Постскрипт и теорема Наполеона
Виктор Кон, 15-08-2018, kohnvict@yandex.ru
15 августа -- день рождения Наполеона. И в этот день один из моих друзей в сети Фейсбук вспомнил о теореме, которую Наполеон якобы доказал. Она геометрическая и я подумал, что было бы интересно доказать ее графически, одновременно написав программу рисунка на языке постскрипт. Она формулируется следующим образом. Если на сторонах произвольного треугольника нарисовать равносторонние треугольники и соединить их центры, то в результате снова получим равносторонний треугольник.
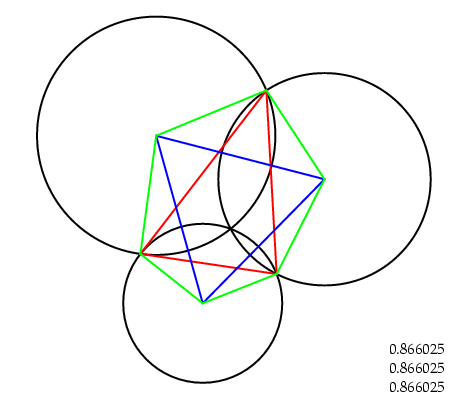
Я поступил иначе. Я сразу нарисовал равносторонний треугольник, вершины которого использовал как центры кругов с общей тройной точкой пересечения. Затем через двойные точки пересечения провел треугольник, который в теореме Наполеона как бы исходный. Ну и осталось проверить, что углы между сторонами треугольника и радиусами кругов равны 30-ти градусам. На самом деле я фиксировал общую точку пересечения кругов как начало координат, задал произвольно две точки равностороннего треугольника и вычислил третью. Затем вычислил точки пересечения кругов и после этого углы.
В данной статье я решил записать как это делается. Полный файл eps рисунка можно посмотреть по ссылке [01]. Итак, начало координат выбрано в тройной точке пересечения кругов. Основную часть программы я записал как процедуру с названием pro1. Задаем произвольно координаты центров двух кругов в переменных x1,y1 и x2,y2. И сразу рисуем два круга, так как мы знаем, что точка (0,0) лежит на окружности. Поэтому радиус первого круга равен R1=sqrt(x1*x1+y1*y1), и круг чертится стандартным образом. Точно так же выглядит код для второго круга.
Далее надо вычислить координаты центра третьего круга. Он должен находиться на одинаковых расстояниях от центров первых двух кругов. Расстояния легко записываются через разности координат и из этого условия определяем y через x как y=--a*x+b, где a=(x2--x1)/(y2--y1), b=(R2*R2-R1*R1)/(2*(y2--y1)). Но это расстояние не может быть произвольным. Оно должно равняться расстоянию между центрами первых двух кругов. Из условия равенства первого расстояния получаем после подстановки y через x, что первое равенство двух расстояний приводит к квадратному уравнению для x вида A*x*x+2*B*x+C=0, где A=(1+a*a),
B=a*y1--a*b--x1, C=b*(b--2*y1)--c, где c=R2*R2--2*x1*x2--2*y1*y2. Это уравнение имеет два решения для двух точек, симметрично расположенных относительно линии между центрами первых двух кругов. Выбор знака зависит от конкретных значений заданных координат и его легко проверить графически. В программе выбран знак плюс потому что очевидно, что третий круг должен быть справа, так как по условию задачи равносторонние треугольники должны быть снаружи от исходного треугольника.
Итак, программа сначала вычисляет параметры a,b,c, затем A,B,C и наконец координату x3=x и y3=--a*x3+b. Теперь легко начертить и третий круг. При этом с графика можно сразу снять точки пересечения кругов. Но нам нужны очень точные значения. Точки пересечения кругов будем обозначать двумя цифрами. Например, точка пересечения кругов 1 и 2 будет иметь координаты x12 и y12. Но при вычислениях можно индексы не писать. Очевидно для координат имеем два уравнения (x--x1)^2+(y--y1)^2=R1*R1 и точно такое же с заменой 1 на 2. Совместное решение уравнений снова дает связь y=--a*x и квадратное уравнение для x, в котором одно решение равно x=0, оно очевидно по определению, а второе решение дает решение x=2*(x1--a*y1)/(1+a*a). В результате получаем координаты для точки 12. Координаты для точек 13 и 23 получаем по тем же формулам с заменой индексов.
Теперь можно красным цветом нарисовать исходный (произвольный) треугольник, синим цветом -- конечный равносторонний треугольник, и зеленым цветом -- радиусы из центров кругов в точки пересечения. Чертеж полностью готов. Но теорема еще не доказана. Нам надо показать, что стороны исходного треугольника являются сторонами правильных треугольников, вписанных в круги. Для этого необходимо вычислить углы между красными и зелеными линиями. Они должны быть равны 30-ти градусам. Углы легко вычисляются через скалярное произведение двух векторов. Например, в первом круге один вектор имеет координаты в виде разности координат точек 13 и 12, а второй вектор -- точек 1 и 12. Вычисляя скалярное произведение и деля на модули векторов получаем косинус первого угла. Точно также получаем косинусы второго и третьего углов.
Значения косинусов записаны в переменные fu1, fu2, fu3. Они преобразуются в текст с помощью команды cvs и показываются на графике. Мы видим значения косинусов 30-ти градусов. Задача решена. Но есть некий немой вопрос. Исходный треугольник может содержать все три вершины совершенно произвольно, то есть 6 параметров. Реально форма треугольника задается 3-я параметрами и еще он может перемещаться по плоскости и вращаться на произвольный угол. У нас же произвольными являются только два центра кругов. То есть 4 параметра. Но еще два параметра -- это тройная точка пересечения. Она фиксирована в начале координат, но могла бы перемещаться по плоскости. Так что все в порядке.
В доказательстве представлена весьма специфическая форма расчетов, но могут быть и другие. В геометрии одно выражается через другое и всегда есть варианты. Я просто хотел показать, что постскрипт вполне способен быстро и относительно просто решать как графические, так и математические задачи. В нем можно не только рисовать, но и делать математические расчеты.
Ссылки на интернет
[01] ![]() EPS файл рисунка для доказательства теоремы Наполеона
EPS файл рисунка для доказательства теоремы Наполеона
.