.

Optics and Lasers in Engineering, Vol. 135, December 2020, 106187

Уравнение транспорта интенсивности: учебное пособие

Chao Zuo, Jiaji Li, Jiasong Sun, Yao Fan, Jialin Zhang, Linpeng Lu, Runnan Zhang, Bowen Wang, Lei Huang, Qian Chen

Когда дело доходит до «измерения фазы» или «количественной фазовой визуализации», многие люди автоматически подразуменвают использование «лазера» и «интерферометрии». Действительно, традиционные методы количественной фазовой визуализации и фазовых измерений обычно основаны на суперпозиции двух лучей с высокой степенью когерентности: сложные интерферометрические конфигурации, строгие требования к стабильности окружающей среды и связанный с этим лазерный спекл-шум серьезно ограничивают их применение в оптической визуализации и микроскопии. С другой стороны, как один из наиболее известных подходов к восстановлению фазы, уравнение переноса интенсивности (TIE) обеспечивает новый неинтерфе-рометрический подход как способ получить доступ к количественной информации о фазе посредством измерения только интенсивности. Несмотря на недостаточность для интерферометрии TIE применим при частично когерентном освещении (например, освещении Келера в обычном микроскопе), обеспечивая оптимальное пространственное разрешение, более высокое соотношение сигнал/шум и лучшее качество изображения. В этом руководстве мы даем обзор основных принципов, областей исследований и типичных применений TIE, уделяя особое внимание оптической визуализации, метрологии и микроскопии. Цель этого руководства двойная. Оно должно служить самостоятельным введением в TIE для читателей, мало или вообще не знающих TIE. С другой стороны, оно пытается дать обзор последних событий в этой области. Эти результаты высвечивают новую эпоху, в которой строгая когерентность и интерферометрия больше не являются ограничениями для количественной фазовой визуализации и дифракционной томографии. Она открывает путь к новому поколению трехмерной микроскопии с применением во всех отраслях биомедицины.

1. Введение

В физике и математике «фазой» периодического сигнала называется скаляр, действительное число, который описывает относительное расположение каждой точки на форме сигнала в пределах каждого полного периода. Фаза обычно выражается как угол (в градусах или радианах) в таком масштабе, что она меняется на один полный оборот по мере прохождения переменной через каждый период. В разделе волновой оптики понятие фазы ограничивается лишь для монохроматического когерентного оптического поля, которое можно описать в терминах двумерного (2D) комплексного показателя с его аргументом, так называемой «фазой» [1,2]. По сравнению с фазой, амплитудную составляющую оптического поля обычно гораздо легче понять, поскольку квадрат амплитуды, также известный как «интенсивность» света (в радиометрии также называемый «светимостью» [3]), является единственным видимым компонентом, который мы можем видеть нашими глазами, представляющим энергию света [4]. Человеческие глаза или датчики изображения могут обнаруживать только компонент интенсивности (или амплитуды) света, но непосредственный доступ к информации о фазе невозможен. Одной из важных причин является то, что частоты колебаний световых волн составляют около 10¹⁴ Гц [5], что намного превышает скорость отклика человеческого глаза (обычно 30 Гц) или фотоэлектрического устройства формирования изображения (частота кадров современной высокоскоростной камеры может достигают только уровня 10⁸ Гц [6]).

Важность фазы можно проиллюстрировать простым и интересным примером из статьи Оппенгейма [7] (см. рис.1). Рассматривая два разных изображения, если мы поменяем местами их фазовые составляющие в частотном спектре, сохраняя при этом их амплитудные компоненты неизменными, то операция Фурье преобразует их спектры обратно в пространственную область и общий внешний вид двух изображений почти поменяется местами. Этот простой пример показывает, что большую часть информации в изображении несет не амплитуда, а фаза (обратите внимание, что этот пример может быть не очень подходящим, поскольку фаза здесь является фазовой составляющей спектра изображения, а не оптической составляющей поля. Важность фазы особенно заметна в некоторых конкретных областях, таких как оптическая метрология, физика материалов, адаптивная оптика, рентгеновская дифракционная оптика, электронная микроскопия и биомедицинская визуализация. Большинство представляющих интерес образцов относятся к фазовым объектам с очень небольшим поглощением, но пространственное распределение их показателя преломления (ПП) или толщины неоднородно. Поэтому они имеют небольшие изменения амплитуды, но сильные изменения фазовых компонент. Человеческие глаза или фотодетекторы чувствительны только к изменению амплитуды, а не к изменению фазы, поэтому они не могут «видеть» фазовый объект напрямую (рис.2). Другими словами, невозможно отличить разные компоненты объекта с различной толщиной или ПП. Таким образом, получение фазовой информации имеет особое значение в таких случаях.

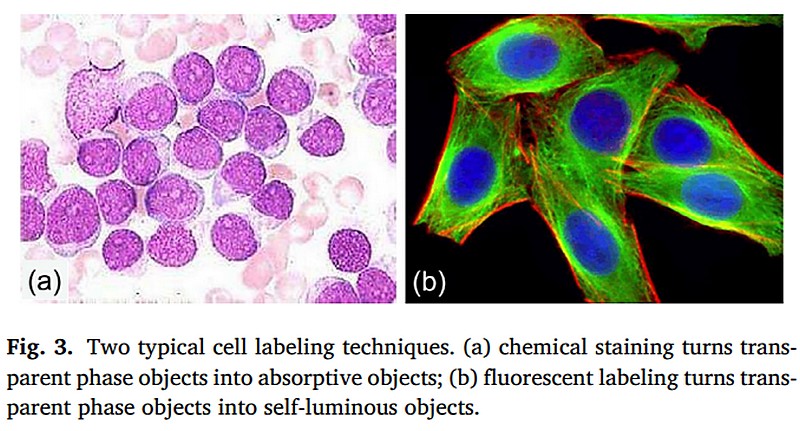
Восстановление фазы является ключевым предметом исследований в области оптических технологий, метрологии и технологии визуализации. Оно играет незаменимую роль как для промышленного контроля, так и для биомедицинской визуализации. Методы фазовой визуализации, особенно для биологических образцов и слабопоглощающих полупрозрачных объектов, имеют долгую историю развития. Цитоплазма и большинство органелл биологических клеток обладают очень слабым поглощением, поэтому они производят очень мало контраста при нормальном освещении в традиционном микроскопе светлого поля. Чтобы преодолеть эту трудность, наиболее распространенным подходом является окрашивание или маркировка. Различные компоненты клетки имеют разное сродство к разным красителям или флуорофорам, создавая достаточный контраст интенсивности или излучая разные спектры флуоресценции (рис.3). Наиболее распространенным методом использования экзогенного контраста является флуоресцентная микроскопия [8], при которой образец метят специфическими флуоресцентными молекулами для получения целевой морфологической информации. Структуру органеллы и белкового комплекса также можно визуализировать в трехмерном виде (3D) с помощью возможностей оптического сечения лазерной конфокальной микроскопии и многофотонной микроскопии [9,10]. С появлением новых флуоресцентных молекулярных зондов и совершенствованием технологий оптической визуализации исследователи разработали множество методов флуоресцентной микроскопии со сверхразрешением, которые превосходят предел разрешения традиционной конфокальной микроскопии, например, микроскопию структурированного освещения (SIM) [11], микроскопию истощения стимулированного излучения (STED) [12], микроскопию фотоактивированной локализации (PALM) [13] и микроскопию стохастической оптической реконструкции (STORM) [14]. Эти методы имеют чрезвычайно высокую точность локализации изображений одиночных молекул или возбуждения флуоресценции и отбеливающих свойств фотоактивируемых флуоресцентных протеинов (белок), значительно превышающую предел разрешения традиционной оптической микроскопии и способную обнаружить наноразмерные структуры флуоресцентно меченных живых клеток. Относительная важность флуоресцентной микроскопии недавно стала очевидной благодаря Нобелевской премии 2014 года по химии за «разработку флуоресцентной микроскопии сверхразрешения». Однако такие методы по-прежнему требуют флуоресцентных красителей и флуоресцентных белков в качестве биомаркеров и поэтому плохо подходят для образцов, которые не флуоресцентны или не могут быть легко помечены флуоресцентно. Кроме того, фотообесцвечивание и фототоксичность флуоресцентных агентов препятствуют визуализации живых клеток в течение длительных периодов времени [15].

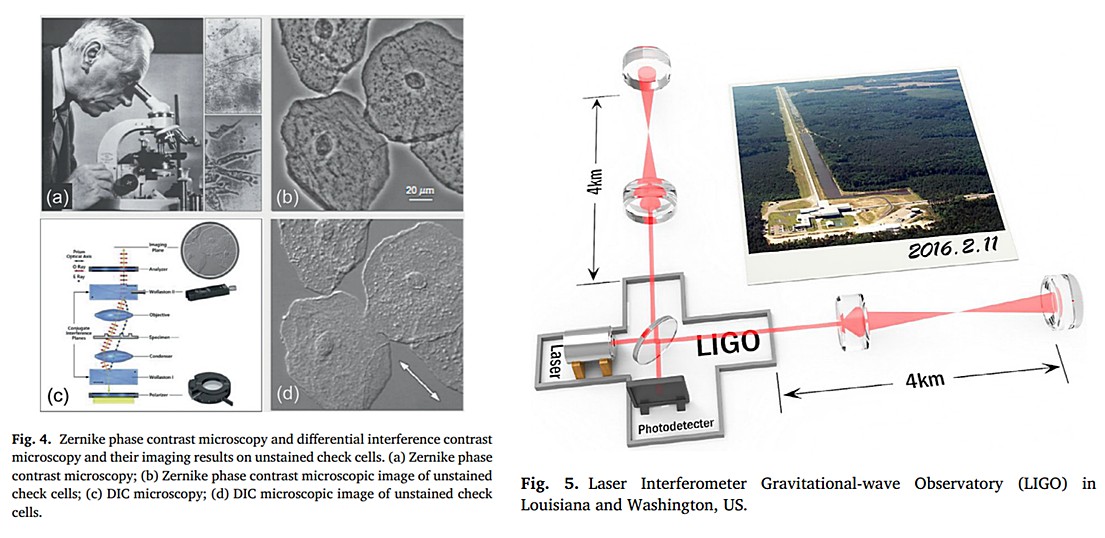
Хотя большинство биологических клеток прозрачны и не изменяют амплитуду проходящего через них света, они вносят фазу задержки из-за разных структурных областей неоднородной оптической плотности (ОП). В 1942 году Цернике [16] изобрел фазовый контраст Цернике (ФКЦ), то есть метод микроскопии [рис.4(а)] для оптической визуализации фазы. В методе используется фазовая маска для смещения только невозмущенной компоненты падающего поля на четверть длины волны, так что она интерферирует с рассеянным полем с более высокими пространственными частотами, обеспечивая максимальный контраст на интерференционном изображении. Это обеспечивает простой и эффективный метод преобразования разности фаз в контраст интенсивностей, что значительно улучшает контраст прозрачного фазового объекта под оптическим микроскопом [рис.4(б)]. Это привело к революции в биологической визуализации, поскольку значительное усиление контраста позволило наблюдать неокрашенные биологические клетки и ткани, которые раньше были почти невидимы, а это изобретение принесло Цернике Нобелевскую премию по физике 1953 года. Несколько позже (в 1952 году) Номарский [17] изобрел микроскопию дифференциального интерференционного контраста (ДИК), основанную на принципе поляризационного расщепления пучка и его сдвига. Фазовый контраст в ДИК-микроскопии пропорционален фазовому градиенту образца вдоль направления сдвига, создавая вид трехмерного физического рельефа, соответствующего изменению оптической плотности образца [рис.4(г)].

Хотя ФКЦ и ДИК представляют собой значительные достижения в микроскопии, все эти методы страдают одним важным недостатком: измеренная интенсивность имеет нелинейную и, следовательно, необратимую связь с фазой образца. Без информации о фазе невозможно определить количественно морфологически значимые количества образца, такие как размер, оптическая толщина, плотность сухой массы и ПП. С другой стороны, артефакты «гало» (рис.4(б)] и «отключения тени» [рис.4(d)], сопровождающие эти методы фазового контраста, также усложняют последующий анализ и обработку изображений (например, подсчет и сегментацию клеток). Эти ограничения в сочетании с появлением цифровых датчиков изображения и достижениями в информационной оптике привели к появлению методов измерения фазы и количественной визуализации фазы (КВФ) [18,19], которые сочетают в себе инновации в оптике, теории визуализации и вычислительных методах, для количественного отображения фазовой информации образца. Количественные фазовые профили клеток позволяют определять клеточную структуру и биофизические параметры с минимальными манипуляциями с образцом. КВФ предлагает важную альтернативу, особенно в тех случаях, когда традиционные методы подготовки, такие как фиксация, окрашивание или флуоресцентные метки, могут повлиять на клеточные функции и ограничить биологическую информацию.

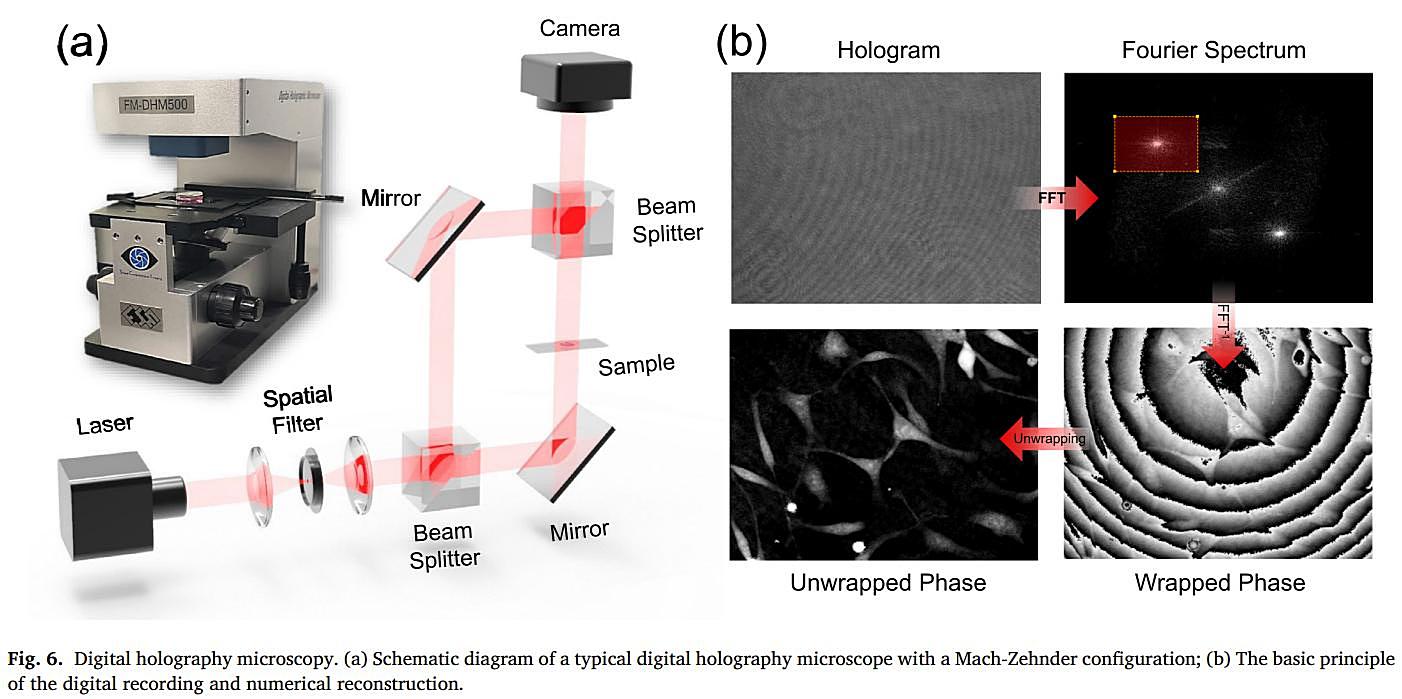
С изобретением лазера и развитием оптической метрологии на протяжении почти полувека наиболее хорошо зарекомендовавшим себя методом измерения фазы является интерферометрия. Поскольку принцип оптической когерентной интерференции впервые оказался потенциальным инструментом измерения в 1880-х годах, интерферометрия сыграла заметную роль в оптической метрологии. В настоящее время высокоточный лазерный интерферометр позволяет осуществлять чрезвычайно чувствительные фазовые измерения с точностью измерения оптического пути до λ/100. Знаменитая лазерная интерферометрическая гравитационно-волновая обсерватория (LIGO) [20,21], обнаружившая гравитационные волны в 2016 году, по сути представляет собой гигантский интерферометр Майкельсона с размахом плеч 4 км (рис.5), позволяющий обнаруживать малейшие изменения расстояния порядка 1/10000 ширины отдельного протона, что представляет собой невероятно малый масштаб влияния, оказываемого проходящими гравитационными волнами. Несмотря на достижения оптической интерферометрии на протяжении десятилетий ее основной принцип остается неизменным: путем наложения дополнительного когерентного опорного луча на исходный объектный луч невидимая информация о фазе может быть преобразована в своего рода сигнал интенсивности, то есть интерференционную картину, которая может быть непосредственно измерена традиционными устройствами обработки изображений. С помощью различных типов алгоритмов анализа полос можно демодулировать фазу из интерферограммы. После десятилетий развития интерферометрия стала более зрелой и породила множество ответвлений, таких как электронная спекл-интерферометрия (ESPI) [22,23], интерферометрическая микроскопия [24–26] и цифровая голография [27–31]. Их основные принципы очень схожи, а развитие практически параллельно. В частности, цифровая голография, благодаря своим уникальным преимуществам и гибкости цифровой записи и численной реконструкции, добилась значительного прогресса за последние два десятилетия и стала эталоном для количественного измерения фазы и микроскопии [32–35] (рис.6). Тем не менее, интерферометрические количественные микроскопические изображения, представленные цифровой голографией и получившие широкое распространение, не поколебали позиции традиционных методов микроскопической визуализации и не смогли вызвать ожидаемую технологическую революцию в науках о жизни. Основные причины кроются в интерферометрических характеристиках «количественного измерения фазы»:

1) Цифровая голографическая микроскопия обычно во многом зависит от источников света с высокой степенью временной когерентности (например, лазер) и пространственной когерентности (например, точечная фильтрация), а также сложных интерферометрических оптических конфигураций (т. е. объектный луч и опорный луч);
2) Из-за обычно используемых источников лазерного освещения цифровая голографическая микроскопия страдает от спекл-шума, возникающего из-за паразитных помех вследствие несовершенства оптической системы, которые не только ограничивают разрешение изображения, но также сильно ухудшают качество изображения;
3) Из-за высокой степени пространственной когерентности источника света разрешение изображения ограничено только пределом когерентной дифракции (половина предела некогерентной дифракции, как в традиционном некогерентном микроскопе);
4) Дополнительный путь опорного луча делает измерения чрезвычайно чувствительными к внешним воздействиям (например, вибрации, быстрому потоку воздуха и т. д.);
5) Фаза, демодулированная из интерферограммы, заворачивается в диапазон (–π, π] (так называемая «обернутая фаза») и необходима дополнительная фазовая развертка для получения истинного абсолютного распределения фазы.

Чтобы устранить или частично облегчить вышеуказанные ограничения традиционных методов интерферометрической визуализации фазы, в последние годы многие исследователи постепенно обратили свое внимание на голографию с низкой когерентностью или интерферометрическую микроскопию в белом свете, например, интерференционную микроскопию пространственного света (SLIM) [36], фазовую микроскопию дифракции белого света (wDPM) [37], четырехволновую интерферометрию бокового сдвига (QWLSI) [38] и τ-интерферометрию [39]. Сочетание широкополосного доступа освещения с общей геометрией пути значительно облегчает проблему когерентного шума и повышает устойчивость к механическим воздействиям, вибрации и колебаниям воздуха, которые обычно влияют на любые интерферометрические системы. Однако большинство из них требуют относительно сложных оптических систем, которые обычно недоступны большинству био/патологов и патологов, что запрещает их широкое использование в биологической и медицинской науке.

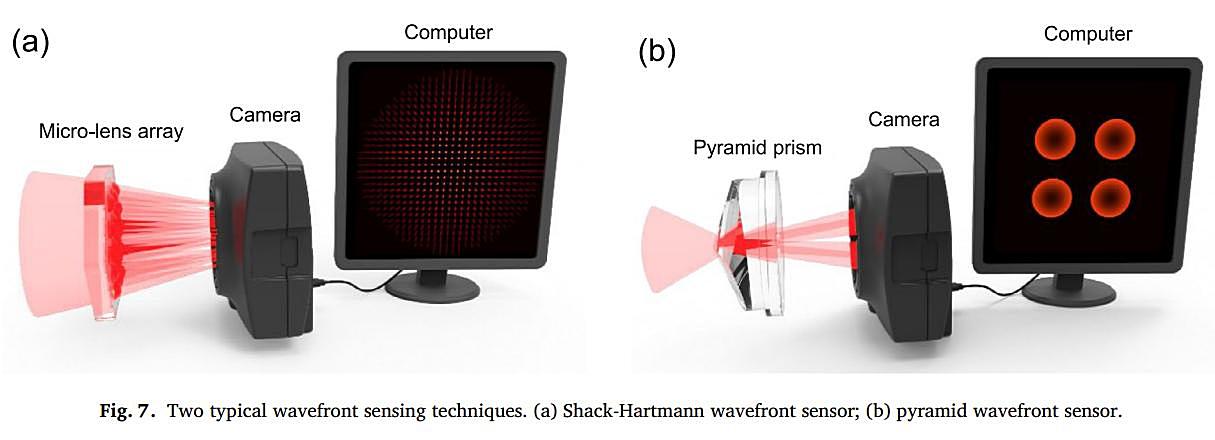
Другая широкая категория методов измерения фазы, не основанная на интерферометрии, известна как неинтерферометрическое измерение фазы. Основная ветвь неинтерферометрических методов измерения фазы называется зондированием волнового фронта, например, датчик волнового фронта Шака-Гартмана [40–42] [Рис.7(a)], пирамидальный датчик волнового фронта [43–45] [Рис.7(b)] и датчик волнового фронта на основе модели [46,47]. Датчик волнового фронта Шака-Гартмана — это метод измерения фазы, основанный на геометрической оптике, который часто используется в системах адаптивной оптики и имеет основные применения в телескопах и астрономических наблюдениях. В таких науках «фазу» часто называют «аберрацией волнового фронта», которая представляет собой разницу между опорным волновым фронтом идеальной оптической системы и искаженным волновым фронтом реальной оптической системы. Первоначальный прототип датчика волнового фронта Шака-Гартмана представляет собой массив отверстий в маске (так называемый экран Хартмана), разработанный астрономом Гартманом [41] в 1900 году. Хотя метод Гартмана имеет простую конструкцию, его точность измерения и эффективность использования света довольно низкая. Позже, в 1971 году, Шак и Платт [40] модифицировали экран Гартмана, заменив апертуры в непрозрачном экране решеткой линз, которая фокусирует входящее излучение в решетку пятен на датчике (см. рис.7 (а)). Интегральный градиент волнового фронта на линзе пропорционален смещению центроида относительно эталонной матрицы пятен с регулярным расстоянием (идеальный случай без аберраций), и тогда распределение волнового фронта (фазы) можно восстановить посредством интегрирования. В настоящее время сфера применения датчика волнового фронта Шака-Гартмана расширилась от астрономических изображений до диагностики качества луча [48,49], оптических испытаний [50,51], атмосферной лазерной связи [52,53], коррекции микроскопических аберраций [54,55]. , офтальмологии [56–58] и т. д. Однако из-за ограничения физического размера микролинзы датчик Шака-Гартмана не в полной мере использует все разрешение пикселей датчика изображения, что приводит к низкому пространственному разрешению восстановленного волнового фронта. Следовательно, датчик волнового фронта Шака-Гартмана редко используется напрямую в качестве инструмента визуализации, особенно в области КВФ и оптической микроскопии.

Другая очень известная и широко используемая технология неинтерферометрического измерения фазы называется восстановлением фазы. Поскольку непосредственно измерить фазу света сложно, но очень легко измерить амплитуду/интенсивность, мы можем рассматривать процесс восстановления (оценки) фазы по распределению интенсивности как математическую «обратную задачу», а решением такой проблемы является так называемый фазовый поиск. Методы фазового поиска можно разделить на две категории: итеративные методы и детерминированные методы. Итеративное восстановление фазы берет свое начало в идеях электронной микроскопии. В 1972 году Герхберг и Сакстон [59,60] предложили первый итеративный алгоритм фазового поиска, называемый алгоритмом Герхберга-Сакстона (GS). Он использует итерационный подход, в котором находится распределение фазы внутри объекта, которое согласуется как с его изображением интенсивности, так и с его картиной дифракции в дальней зоне. Было обнаружено, что предложенный алгоритм способен прийти к правильному решению, и впоследствии лежащие в его основе идеи были применены к широкому кругу областей, таких как рентгеновская дифракционная визуализация [61–64] (также называемая когерентным дифракционным изображением, КДИ) [рис.8(а)], адаптивная оптика [65,66] и количественная фазовая микроскопия [67–71]. Практическая проблема рентгеновской визуализации заключается в том, что рассеяние объекта настолько слабое, что нерассеянный луч заглушает интересующий сигнал. Эта проблема смягчается введением ограничителя луча, чтобы предотвратить разрушение детектора недифрагированным лучом за счет значительной потери информации на низких пространственных частотах. Мияо и др. [61] обошли эту проблему, используя дополнительное электронно-микроскопическое изображение объекта для воссоздания недостающих данных о низких пространственных частотах, и экспериментально продемонстрировали обоснованность этого подхода с помощью рентгеновских данных. Быстрый рост интереса к КДИ во многом был обусловлен работой Мияо и др. [61].

Однако алгоритм GS также имеет свои проблемы и ограничения. Некоторые проблемы могут быть результатом самого итерационного алгоритма, например, сходимость алгоритма стагнирует после первых итераций или даже попадает в локальный минимум [72–74]. Были предложены различные модифицированные алгоритмы для улучшения сходимости исходного алгоритма GS. В 1973 году Мизелл [75] указал, что алгоритм GS применим не только для распределения интенсивности в плоскости изображения и в плоскости Фурье в дальнем поле, но также может быть расширен до двух или более дифракционных картин с разными расстояниями распространения. Затем он использовал дополнительные ограничения интенсивности, чтобы повысить точность и сходимость итерационного алгоритма. По сравнению с исходным алгоритмом GS модифицированный алгоритм Мизелла является более гибким и практичным, что открывает новые идеи для улучшения итеративного алгоритма поиска фазы. До сих пор появляются новые улучшенные и оптимизированные алгоритмы с использованием различных методов, таких как несколько расстояний распространения [76,77], несколько длин волн освещения [78], фазовая модуляция [79,80] и модуляция спекл-освещения [81,82]. При решении обратных задач присущи и другие проблемы алгоритма GS, такие как вопрос о существовании и единственности решения [83–86]. Понятно, что если объект настолько мал, что изображение в ближнем поле не может быть получено (доступна только дифракционная картина в дальней зоне), то реконструкция с помощью алгоритма GS невозможна. В общем случае, не существует однозначного соответствия между 2D-сигналом и его величиной Фурье (разные объекты могут создавать одинаковые дифракционные картины в дальней зоне), и, следовательно, проблема некорректна. Бейтс [83] рассмотрел эту проблему и заявил (без доказательства), что объект может быть однозначно определен по его автокорреляционной функции (т. е. по картине дифракции в дальней зоне), если известна его пространственная протяженность (за исключением нескольких неважных случаев, таких как сдвиг, фазовое сопряжение, то есть обращение волнового фронта, и инверсия). В 1982 году, после тщательного анализа принципа оптимизации алгоритма GS, Фиенап [87] отметил, что GS эквивалентен алгоритму уменьшения ошибок, который по сути аналогичен алгоритму наискорейшего спуска. Работа Фиенапа [87] заложила прочную теоретическую основу для решения проблемы фазового восстановления с точки зрения выпуклой оптимизации. Это также дает разумное объяснение проблеме застоя: из-за невыпуклости самой задачи восстановления фазы нет никакой гарантии, что алгоритм уменьшения ошибок сможет наконец достичь глобального минимума. Фиенап [87,88] продемонстрировал, что модификация алгоритма GS, основанная на теориях кибернетики, так называемый гибридный алгоритм ввода-вывода (HIO), может помочь предотвратить застревание итерационного алгоритма в локальных минимумах, где используется только вспомогательная информация, используемая на предметной плоскости. Этот алгоритм привел к ряду анализов и улучшений, в первую очередь в способе обновления оценки объекта. К ним относятся гибридное проекционное отражение [89], разностная карта [90], релаксированные усредненные переменные отражения [91] и переворот заряда [92]. Хотя все эти идеи кажутся простыми в реализации, их успешное применение к экспериментальным данным требует значительных навыков и опыта. Единый анализ методов был опубликован Марчезини [93], в котором предполагается, что ни один из них не дал алгоритма, который сходился во всех случаях. Еще одно важное нововведение, предложенное Марчезини и др. [63] представляет собой так называемый алгоритм «обертывания», в котором поддержка объекта уточняется динамически. Этот метод очень полезен для восстановления распределения атомов внутри нанокристаллов.

Птихография — это еще один итеративный подход к фазовому восстановлению, берущий свое начало в электронной микроскопии [94]. В 2004 году Роденбург и Фолкнер [95,96] ввели идею «птихографии» в алгоритмы GS и HIO и представили новый итеративный метод поиска фазы, так называемый птихолографический итерационный двигатель (PIE). При реализации птихографии объект освещается полем, ограниченным по протяженности, и регистрируется дифракционная картина, как показано на рис.8(б). Этот процесс повторяется до тех пор, пока интересующая область не будет полностью просканирована. Полученные в результате пространственно перекрывающиеся «подапертурные» дифракционные картины используются в качестве ограничений интенсивности, а сложное распределение амплитуды в области, охваченной пучком, может быть восстановлена с помощью итеративного алгоритма восстановления фазы, аналогичного GS и HIO. По сравнению с GS и HIO, восстановление птихографической фазы является более стабильным и надежным из-за высокой избыточности данных, возникающей из-за большого количества собранных пространственно перекрывающихся данных об интенсивности. Следовательно, невыпуклость задачи восстановления фазы эффективно смягчается и устраняется неоднозначность между истинным решением и сопряженным к нему [86]. В последующее десятилетие методы птихографического восстановления фазы были тщательно изучены и усовершенствованы, а значительный прогресс был достигнут в восстановлении зондовой функции освещения [97–102], коррекции позиционных ошибок [103–105], когерентном модовом разложении [106–109], улучшении разрешения [110–113] и разделения по глубине многослойных образцов [114–117]. В настоящее время он стал важным подходом для рентгеновской дифракции высокого разрешения [118–120], электронной микроскопии [121–123], а также оптической фазовой визуализации и микроскопии [124–126].

В 2013 году Чжэн и др. [127] расширили птихографию из пространственной области в частотную область, представив ее двойной аналог, названный фурье-птихографической микроскопией (FPM). В методе FPM «птихография» существует в области Фурье: образец больше не сканируется в пространственной области пучком с ограниченной апертурой, а последовательно освещается плоскими волнами под разными углами (обычно с помощью светодиодной матрицы); изображения интенсивности не получаются в дальнем поле (область Фурье), а представляют собой сфокусированные изображения низкого разрешения, снятые непосредственно в пространственной области. Конечная апертура системы формирования изображений становится «субапертурой» в частотной области, в то время как изменения угла освещения позволяют осуществлять перекрывающееся сканирование субапертуры в частотной области, как показано на рис.9. Из-за идеальной двойственности ключевые вопросы FPM, такие как коррекция аберраций [128], коррекция позиционных ошибок [129,130], когерентное модовое разложение [131–133], разделение по глубине для многослойных образцов [134,135], последовательно решались за последние несколько лет. В настоящее время он развивается практически параллельно с традиционной (пространственной) птихографией. Элегантность метода FPM заключается в том, что он не только извлекает информацию о фазе образца, но и естественным образом обеспечивает синтезированную апертуру наряду с процессом птихографического обновления в частотной области, эффективно улучшая разрешение изображения [130,136,137]. Как правило, объектив с малым увеличением и низкой числовой апертурой (NA) используется в FPM для получения собственного большого поля зрения (FOV), а затем для синтезированной апертуры используется освещение с большим углом. Конечная эффективная числовая апертура представляет собой сумму числовой апертуры объектива и числовой апертуры освещения под наибольшим углом, и, таким образом, FPM обычно обеспечивает очень большое произведение изображения на пространственную полосу пропускания (SBP). Например, в 2017, Сан и др. [138] сообщили о платформе FPM с улучшенным разрешением (reFPM) на основе освещения с высокой числовой апертурой, в которой цифровой масляно-иммерсионный конденсатор на основе светодиодной матрицы используется для создания программируемого плосковолнового освещения под большим углом, наделяя объектив с числовой апертурой 10×0.4 свойствами эффективной визуализации с числовой апертурой 1.6 (латеральное разрешение 308 нм для когерентной визуализации) при широком поле зрения 2.34 мм² (рис.9).

Как упоминалось выше, итеративный поиск фазы эффективно решает проблему «прямой реконструкции фазы по измерениям интенсивности» и способствует переходу от интерферометрического измерения фазы к неинтерферометрическому. В частности, итеративное восстановление фазы на основе дефокусировки и птихографическая визуализация внесли значительный вклад в развитие и прогресс адаптивной оптики, рентгеновской дифракционной визуализации и электронной микроскопии. Однако по-прежнему существуют два ограничения: (1) для обеспечения стабильной конвергенции часто требуется большой объем данных об интенсивности; (2) для получения надежного решения необходимо большое количество итераций. Эти два недостатка исключают их использование для высокоскоростных приложений обработки изображений в реальном времени. Кроме того, алгоритмы восстановления фазы связывают рассеянное поле на объекте с рассеянным полем на детекторе посредством преобразования Фурье, соотношение, которое справедливо только для полностью когерентного оптического поля. Таким образом, надежная реконструкция критически зависела от очень высокой степени когерентности [139], что является предположением, которое не справедливо для многих частично когерентных источников.

В отличие от итеративных методов, другая категория методов восстановления фазы использует распространение для прямого восстановления фазы неитеративным способом. Вероятно, эту идею впервые предложил Тиге [140,141]. В 1982 году он впервые указал, что в параксиальном приближении можно использовать закон сохранения энергии при распространении (уравнение Гельмгольца) для вывода эллиптического уравнения в частных производных второго порядка, которое описывает количественную связь между изменением интенсивности вдоль оптической оси и фазой оптического поля в плоскости, перпендикулярной оптической оси [140]. Тиге считал, что это уравнение можно использовать в качестве подхода к восстановлению фазы. Он назвал это уравнение уравнением переноса интенсивности (TIE), и это будет основной темой данного учебного пособия. В своей последней статье 1983 г. Тиге [141] предложил предварительный подход к решению уравнения, основанного на функциях Грина. В отличие от итеративных методов восстановления фазы, TIE не использует традиционную скалярную формулу дифракции для итеративного восстановления фазы. Если известны распределения интенсивности в плоскости фокуса (измеренное непосредственно) и производная осевой интенсивности (оцененная по конечной разнице между двумя дефокусированными интенсивностями), информацию о фазе можно получить напрямую (детерминированно) путем решения TIE без итерационных операций. По сравнению с традиционным интерферометрическим методом метод TIE имеет множество уникальных преимуществ: неинтерферометричность (без использования опорного луча), простой расчет (без итераций), возможность частично когерентных во времени и пространстве пучков (например, светодиодное освещение, галогенная лампа и встроенное освещение Келера обычные микроскопы), не требует фазовой развертки (непосредственное получение абсолютной фазы), сложных оптических установок и стабильной среды измерения.

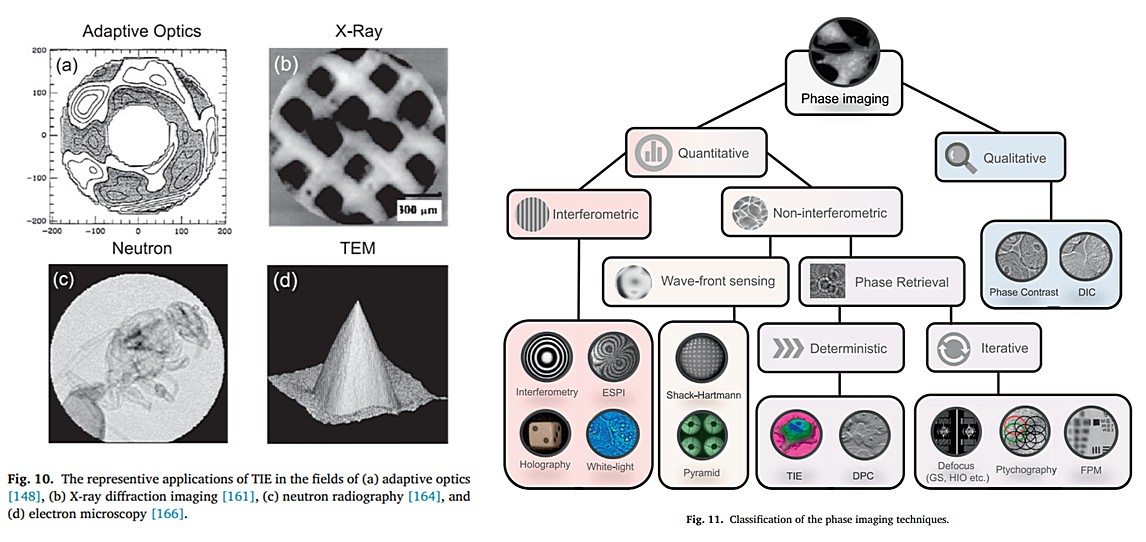
Вскоре после этого, в 1984 году, Штрейбл [142] обнаружил, что TIE применим к оптической микроскопии в качестве инструмента для фазово-контрастного изображения прозрачных фазовых объектов. Поскольку численное решение TIE в то время не было предложено, он продемонстрировал только эффект усиления фазового градиента неокрашенных клеток, взяв производную осевой интенсивности. Тем не менее, эта новаторская работа заложила предварительную теоретическую основу для последующего широкого применения TIE в области оптической микроскопии. В 1988 году Итикава и Такеда [143] впервые экспериментально подтвердили TIE. Они решили TIE методом преобразования Фурье и получили количественное распределение фазы одномерного образца. Однако вместо решения уравнения в частных производных этот метод оказался лишь частным случаем решеточной сдвиговой интерферометрии [144]. Параллельно исследовательская группа Гавайского университета под руководством Родье [144–148] также изучала возможности использования TIE для коррекции искажения волнового фронта, вносимого атмосферной турбулентностью, в адаптивной оптике [рис.10(а)]. Предполагая, что амплитуда волнового поля почти однородна, TIE можно упростить из более сложного эллиптического уравнения в частных производных до стандартного уравнения Пуассона. Это уравнение Пуассона показывает, что производная осевой интенсивности оптического поля пропорциональна кривизне его волнового фронта (вторая производная, т. е. лапласиан), поэтому этот метод часто называют измерением кривизны (CS). Нет сомнений в том, что исследовательская работа Роддье значительно продвинула метод поиска фазы с помощью TIE. Вклад Родье состоит не только в применении TIE к адаптивной оптике, но, что более важно, он впервые предложил численные решения упрощенной формы TIE, основанные на методе последовательной сверхрелаксации (SOR) [145] и методе итеративного преобразования Фурье [149]. В 1988 году Роддье оценил производную осевой интенсивности, измерив сфокусированные и слегка дефокусированные сигналы интенсивности на входном зрачке телескопа, и подал их непосредственно обратно в схему деформируемого зеркала, чтобы исправить искажение атмосферного волнового фронта в реальном времени [145,146]. Затем, в 1991 году, Роддье [150] построил 13-блочную адаптивную оптическую систему, чувствительную к кривизне низкого порядка, и представил предварительные результаты лабораторных экспериментов. Дефокусировка осуществлялась посредством быстрой вибрации мембранного зеркала с переменной кривизной, так что интенсивности перефокусировки и недофокусировки можно было измерить одновременно. Сигнал кривизны волнового фронта измерялся с помощью лавинной фотодиодной матрицы, а управление деформируемым зеркалом осуществлялось на основе метода управления матрицей отклика. Впоследствии измерение кривизны получило широкое распространение в США [CFHT (телескоп Канада-Франция-Гавайи) с апертурой 3,6 м [151] и телескоп Gemini North диаметром 8 м [152]], и в Европе [телескоп с апертурой 8,2 м. VLTI (Интерферометр Очень Большого Телескопа)] [153], а также в Японии (8,2-мапертурный Телескоп Субару) [154], и на станциях крупных астрономических телескопов других стран.

Во второй половине 1990-х годов теоретический аспект TIE развивался очень быстро и принес плодотворные достижения, причем основной движущей силой была исследовательская группа по рентгеновской дифракционной визуализации Мельбурнского университета. В 1995 году Гуреев и др. [155] впервые доказали корректность и единственность решения задачи TIE на основе строгой математики: если интенсивность оптического поля строго больше 0 (исключая случай оптического вихря) и при соответствующих граничных условиях, решение TIE существует и единственно (для граничного условия Неймана решение единственное с точностью до тривиальной аддитивной константы). Эта работа заложила теоретическую основу для последующего извлечения фазы TIE и приложений КВФ. В 1996 году Гуреев и Ньюджент [156,157] предложили решать TIE на основе ортогонального разложения, такого как полиномиальное разложение Цернике или разложение Фурье, и отметили, что когда распределение интенсивности однородно, TIE можно решить с помощью быстрого преобразования Фурье (БПФ)[158]. Вскоре после этого Паганин и Ньюджент [159] расширили решение на основе БПФ, чтобы его можно было эффективно адаптировать к случаю неравномерного распределения интенсивности. Этот простой и эффективный метод, основанный на БПФ, в настоящее время стал наиболее широко используемым численным решением TIE. Создание математической основы для численного решения TIE стало мощным автомобилем, который мотивирует его быстрое развитие и широкое применение в различных областях. В 1995 г. Снигирев и др. [160] обнаружили, что методы неитеративного восстановления фазы на основе распространения могут быть применены в области рентгеновской визуализации. Вскоре после этого, в 1996 г., Ньюджент [161] и др. сообщили о количественном фазовом изображении тонкой углеродной фольги с использованием жесткого рентгеновского излучения с энергией 16 кэВ на основе TIE [рис.10(б)]. Эти работы вызвали бурный рост интереса TIE к приложениям рентгеновской оптики [162,163]. Впоследствии применение TIE распространилось и на область нейтронной радиографии [164, 165] [Рис.10(в)] и просвечивающую электронную микроскопию (ПЭМ) [166–174] [рис.10(г)]. Общей чертой этих наук является то, что трудно получить высококогерентный источник излучения, поэтому TIE стал простой и эффективной альтернативой интерферометрии.

В конце 1990-х годов, с одной стороны, теоретическая основа TIE была уже прочно установлена; с другой стороны, исследователи, занимающиеся КВФ, все больше осознавали важность использования освещения с низкой когерентностью для улучшения разрешения и качества изображения. Эти два аспекта затем стали катализатором широкого применения TIE в области оптической визуализации и микроскопии. В 1998 году Паганин и Ньюджент [159] по-новому интерпретировали значение термина «фаза» частично когерентных полей и указали, что это скалярный потенциал, градиент которого соответствует усреднённому по времени вектору Пойнтинга. Важность данной работы состоит в том, что она дает более обобщенное и содержательное определение «фазы», закладывая теоретическую основу для последующего восстановления фазы методом TIE при частично когерентном освещении. В том же году Барти и др. [175] кратко сообщили о результатах КВФ клеток щеки и оптических волокон на основе TIE, что было первым появлением TIE в количественной оптической фазово-контрастной визуализации. Затем Барти и др. [176] распространили этот метод на количественную фазовую томографию, основываясь на том же подходе, что и «голотомография», ранее продемонстрированная Cloetens et al. [163] в 1999 г. Благодаря успешным применениям в области КВФ и оптической микроскопии в начале 20-го века теория восстановления фазы методом TIE случайно совпала с теорией оптической передаточной функции (OTF) в оптической микроскопии. В 2002 году Барон, Ньюджент и др. [177] теоретически проанализировали формирование изображений слабофазовых объектов под оптическим микроскопом на основе теории 3D OTF, разработанной Штриблом [178], и дополнительно подтвердили применимость TIE при частично пространственно-когерентном освещении. В том же году Шеппард [179] проанализировал восстановление фазы TIE в рамках борновского приближения первого порядка и отметил, что низкочастотная составляющая осевой производной интенсивности пропорциональна фазовому лапласиану (производной второго порядка). Вывод согласуется со случаем упрощенной версии TIE при равномерной интенсивности, проанализированным Роддье [144–146]. Первоначальная разработка TIE в области оптической микроскопии и экспериментальные результаты Барти и др. возглавили применение TIE в области биологической и биомедицинской визуализации. Керл и др. [180,181] использовали TIE для количественного определения морфологии и скорости роста клеток, указывая на то, что количественная фазовая информация очень способствует обработке данных и количественному анализу, такому как сегментация и подсчет клеток. Росс и др. [182] использовали TIE для повышения контрастности изображений неокрашенных клеток при облучении микролучами. Драгомир и др. [183] успешно применили TIE для количественного измерения эффекта двойного лучепреломления неокрашенных изолированных кардиомиоцитов. Метод TIE не ограничивался только биологическими образцами, но также успешно применялся для количественного измерения распределения фазы и ПП в оптических волокнах и других технических фазовых объектах [184–187].

С 2010 года по настоящее время восстановление фазы методом TIE достигло нового расцвета благодаря блестящим достижениям в области изображений в видимом свете и микроскопии. За этот период базовая теория TIE (особенно теория частично когерентной визуализации) и связанные с ней приложения (особенно приложения количественной фазовой микроскопии и томографии) снова сделали большой шаг вперед, достигнув новых и беспрецедентных высот. Коу и др. [188] продемонстрировали, что метод TIE может быть непосредственно реализован на основе стандартного ДИК-микроскопа для реализации КВФ и успешно получил количественные фазовые изображения клеток щеки человека. В том же году Уоллер и др. [189] предложили метод, названный TIE высокого порядка, с использованием большего количества измерений интенсивности в нескольких дефокусированных плоскостях для повышения точности и надежности восстановления фазы. Простое и понятное описание этих работ значительно повысило популярность TIE в области оптической визуализации и микроскопии. Между тем, Уоллер и др. также предложили однокадровые оптические конфигурации метода TIE, основанные на объемной голографии [190] и хроматической аберрации [191], позволяющие получать изображения интенсивности на разных расстояниях дефокусировки за одну экспозицию. В 2011 году Коу и др. [192] предложили метод деконволюции OTF для КВФ при частично когерентном освещении и количественно сравнили его с традиционным методом TIE. В 2012 году Альморо и др. [193] использовали подсветку спекл-поля для повышения фазового контраста расфокусированных по интенсивности изображений гладких объектов. В том же году Горти и Шенбрун [194] впервые применили TIE для проточной цитометрии и реализовали автоматический сбор изображений с интенсивностью сквозь фокус путем наклона микрофлюидного канала вертикально. В то же время существует большое количество публикаций, посвященных оптимизации восстановления фазы конечно-разностной схемой для повышения точности и устойчивости TIE в условиях шума [195–200]. С 2012 года наша группа проводит систематическую исследовательскую работу по фазовому восстановлению TIE, при этом тщательно и всесторонне изучены несколько ключевых теоретических вопросов TIE:

1) Эффективное численное решение в неоднородных граничных условиях [201–203];
2) Анализ и компенсация фазового расхождения [204];
3) Оптимальная оценка производной осевой интенсивности [205, 206];
4) Расширение фазового пространства для частично когерентных полей [207, 208];
5) Повышение разрешения за счет светотехники [209–211].
6) Дифракционная томография при частично когерентном освещении [212–214];

В экспериментальных аспектах вместо включения системы механической перефокусировки (например, пьезо-стола) для обеспечения сквозного сканирования мы предложили ввести электрически перестраиваемую линзу [215] или пространственный модулятор света (ПМС) [216], помещенный в Фурье-сопряженную плоскость детектора в обычном широкопольном просвечивающем микроскопе. Это обеспечивает быстрое и высокоскоростное получение стека интенсивностей сквозь фокус, что делает возможным динамическую визуализацию фазы TIE для живых клеток. Мы успешно применили эти системы для исследования морфологических изменений и фагоцитоза макрофагов, вызванных лекарствами [216], визуализации клеточной динамики раковых клеток [215, 217] и характеристики микрооптических элементов [202]. На сегодняшний день вычисление фазы методом TIE привлекает все больше и больше внимания как со стороны научных кругов, так и со стороны промышленности, и связанные с этим новые теории и технологии все еще постоянно появляются.

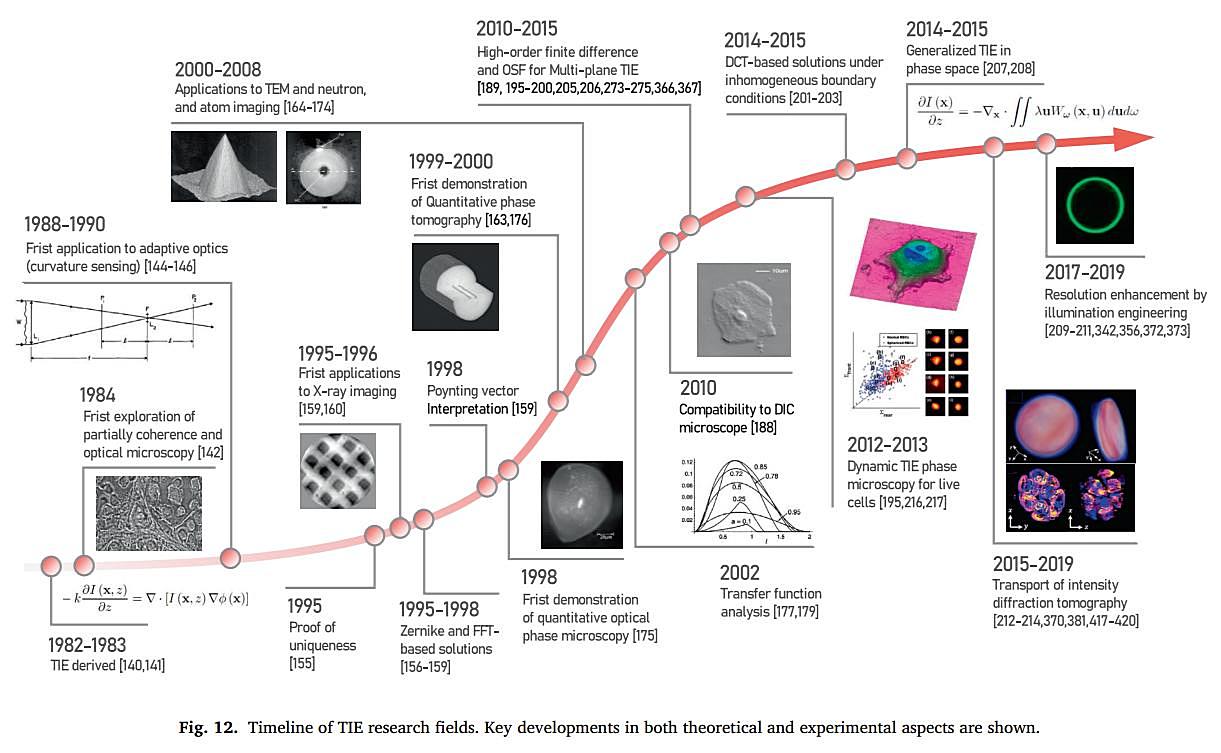
Как упоминалось ранее, мы кратко обобщили развитие технологий фазовой визуализации и измерений, предполагая, что эти технологии можно разделить на две основные категории: метод фазовой визуализации (фазово-контрастное изображение) и метод измерения фазы (количественное фазовое изображение). Существенная разница между этими двумя категориями заключается в том, могут ли они восстановить «количественную» фазовую информацию. Что касается измерения фазы, его также можно разделить на интерферометрию, измерение волнового фронта и определение фазы. Интерферометрия и фазовый поиск также имеют свои независимые подотрасли. На рис.11 показана классификация технологий фазовой визуализации и измерений. В следующих частях акцент будет сделан на технологии неинтерферометрического измерения фазы на основе TIE. Как обсуждалось выше, хотя в последние годы широко сообщалось о фазовом восстановлении и количественной фазовой микроскопии на основе TIE, не было нового всестороннего обзора TIE, фокусирующегося на основных принципах, технических деталях и практическом применении этой новой технологии. Таким образом, в настоящее время, похоже, настал момент для этого руководства, в котором подробно и всесторонне описываются фундаментальные принципы и последние достижения TIE, представляющие интерес для сообщества ученых-оптиков и инженеров, физиков и биологов, заинтересованных в в оптической микроскопии и фазовой визуализации. Прежде чем мы начнем, на рис.12 показан график развития исследований TIE, на котором представлен обзор соответствующих областей исследований и обобщены ключевые разработки как в теоретическом, так и в экспериментальном аспектах. Мы также включили в начало таблицы 1 и 2 со списком всех сокращений, обозначений и символов, используемых в руководстве.

Остальные части этой статьи организованы следующим образом: В разделе 2 мы начинаем с мотивов разработки TIE, описываем его фундаментальный принцип, обрисовываем его выводы и физические последствия. В разделах 3–8 подробно обсуждаются несколько ключевых теоретических вопросов TIE, включая их решения, модель формирования изображения при когерентном освещении, оценку производной осевой интенсивности, КВФ при частично когерентном освещении и трехмерную дифракционную томографию, основанную на переносе интенсивности. В разделе 9 представлены конфигурации системы и типичные применения TIE с упором на оптические изображения, метрологию и микроскопию в диапазоне видимого света. Наконец, в разделе 10 изложены сложные проблемы, а также будущие направления исследований.

Список ссылок

[1] Cowley JM. Diffraction physics. Elsevier; 1995.
[2] Goodman JW. Introduction to Fourier Optics. Roberts and Company Publishers; 2005.
[3] Griffiths D.J.. Introduction to electrodynamics. 2005.
[4] Hecht E. Optics. 4 edition. Reading, Mass: Addison-Wesley; 2001. ISBN 978-0-8053-8566-3.
[5] Born M, Wolf E, Bhatia AB, Clemmow PC, Gabor D, Stokes AR, Taylor AM, Wayman PA, Wilcock WL. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. 7th edition. Cambridge ; New York: Cambridge University Press; 1999. ISBN 978-0-521-64222-4.
[6] High-speed camera. 2017. Page Version ID: 786672531;
[7] Oppenheim AV, Lim JS. The importance of phase in signals. Proceedings of the IEEE 1981;69(5):529–41.
[8] Giloh H, Sedat JW. Fluorescence microscopy: reduced photobleaching of rhodamine and fluorescein protein conjugates by n-propyl gallate. Science 1982;217(4566):1252–5.
[9] Webb RH. Confocal optical microscopy. Rep Prog Phys 1996;59(3):427.
[10] Diaspro A, et al. Confocal and two-photon microscopy: foundations, applications, and advances, vol 1. Wiley-Liss New York; 2002.
[11] Gustafsson MG. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J Microsc 2000;198(Pt 2):82–7.
[12] Hell SW, Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt Lett. 1994;19(11):780–2.
[13] Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006;313(5793):1642–5.
[14] Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat Methods 2006;3:793–6. doi:10.1038/nmeth929.
[15] Stephens DJ, Allan VJ. Light microscopy techniques for live cell imaging. Science 2003;300(5616):82–6.
[16] Zernike F. Phase contrast, a new method for the microscopic observation of transparent objects. Physica 1942;9:686–98.
[17] Nomarski G. Differential microinterferometer with polarized waves; 1955. 9S–11S.
[18] Popescu G. Quantitative Phase Imaging of Cells and Tissues. McGraw-Hill Professional; 2011.
[19] Park Y, Depeursinge C, Popescu G. Quantitative phase imaging in biomedicine. Nat Photonics 2018;12(10):578–89.
[20] Abramovici A, Althouse WE, Drever RW, Grsel Y, Kawamura S, Raab FJ, Shoemaker D, Sievers L, Spero RE, Thorne KS, Vogt RE, Weiss R, Whitcomb SE, Zucker ME. Ligo: The laser interferometer gravitational-wave observatory. Science 1992;256(5055):325–33.
[21] Collaboration LS, Collaboration V. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys Rev Lett 2016;116(6):061102.
[22] Lekberg O. Electronic speckle pattern interferometry. Phys in Tech 1980;11(1):16.
[23] Wang W-C, Hwang C-H, Lin S-Y. Vibration measurement by the time-averaged electronic speckle pattern interferometry methods. Appl Optics 1996;35(22):4502–9.
[24] Schwarz CJ, Kuznetsova Y, Brueck SRJ. Imaging interferometric microscopy. Opt Lett 2003;28(16):1424–6.
[25] Popescu G, Ikeda T, Dasari RR, Feld MS. Diffraction phase microscopy for quantifying cell structure and dynamics. Opt Lett 2006;31(6):775–7.
[26] Kuznetsova Y, Neumann A, Brueck SRJ. Imaging interferometric microscopy–approaching the linear systems limits of optical resolution. Opt Express 2007;15(11):6651–63.
[27] Cuche E, Bevilacqua F, Depeursinge C. Digital holography for quantitative phase–contrast imaging. Opt Lett 1999a;24(5):291–3.
[28] Cuche E, Marquet P, Depeursinge C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl Optics 1999b;38(34):6994–7001.
[29] Cuche E, Marquet P, Depeursinge C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography. Appl Optics 2000;39(23):4070–5.
[30] Schnars U, Jptner WPO. Digital recording and numerical reconstruction of holograms. Meas Sci Technol 2002;13(9):R85.
[31] Schnars U, Jueptner W. Digital holography: digital hologram recording, numerical reconstruction, and related techniques. Springer Science & Business Media; 2005.
[32] Marquet P, Rappaz B, Magistretti PJ, Cuche E, Emery Y, Colomb T, Depeursinge C. Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt Lett 2005;30(5):468–70.
[33] Kemper B, Langehanenberg P, Von Bally G. Digital holographic microscopy: A new method for surface analysis and marker-free dynamic life cell imaging. Optik Photonik 2007;2(2):41–4.
[34] Kemper B, Bally Gv. Digital holographic microscopy for live cell applications and technical inspection. Appl Optics 2008;47(4):A52–61.
[35] Kim MK. Digital holographic microscopy. In: Digital Holographic Microscopy. Springer; 2011. p. 149–90.
[36] Wang Z, Millet L, Mir M, Ding H, Unarunotai S, Rogers J, Gillette MU, Popescu G. Spatial light interference microscopy (SLIM). Opt Express 2011;19(2):1016–26.
[37] Bhaduri B, Pham H, Mir M, Popescu G. Diffraction phase microscopy with white light. Opt Lett 2012;37(6):1094–6.
[38] Bon P, Maucort G, Wattellier B, Monneret S. Quadriwave lateral shearing interferometry for quantitative phase microscopy of living cells. Opt Express 2009;17(15):13080–94.
[39] Girshovitz P, Shaked NT. Compact and portable low-coherence interferometer with off-axis geometry for quantitative phase microscopy and nanoscopy. Opt Express 2013;21(5):5701–14.
[40] Shack RV. Production and use of a lecticular hartmann screen. J Opt Soc Am 1971;61:656–61.
[41] Hartmann J. Bemerkungen uber den bau und die justirung von spektrographen. Zt Instrumentenkd 1990;20(47):17–27.
[42] Platt BC, Shack R. History and principles of shack-hartmann wavefront sensing. J Refract Surg 2001;17(5):S573–7.
[43] Ragazzoni R. Pupil plane wavefront sensing with an oscillating prism. J Mod Opt 1996;43(2):289–93.
[44] Esposito S, Riccardi A. Pyramid wavefront sensor behavior in partial correction adaptive optic systems. Astron Astrophys 2001;369(2):L9–L12.
[45] Ragazzoni R, Diolaiti E, Vernet E. A pyramid wavefront sensor with no dynamic modulation. Opt Commun 2002;208(1-3):51–60.
[46] Neil MAA, Booth MJ, Wilson T. New modal wave-front sensor: a theoretical analysis. J Opt Soc Am A 2000;17:1098–107.
[47] Booth MJ. Wave front sensor-less adaptive optics: a model-based approach using sphere packings. Opt Express 2006;14:1339–52.
[48] Schfer B, Mann K. Determination of beam parameters and coherence properties of laser radiation by use of an extended hartmann-shack wave-front sensor. Appl Optics 2002;41:2809–17.
[49] Schfer B, Lbbecke M, Mann K. Hartmann-shack wave front measurements for real time determination of laser beam propagation parameters. Rev Sci Instrum 2006;77:053103.
[50] Pfund J, Lindlein N, Schwider J, Burow R, Blmel T, Elssner KE. Absolute sphericity measurement: a comparative study of the use of interferometry and a shack-hartmann sensor. Opt Lett 1998;23:742–4.
[51] Greivenkamp JE, Smith DG, Gappinger RO, Williby GA. Optical testing using shack--hartmann wavefront sensors. In: Optical Engineering for Sensing and Nanotechnology (ICOSN 2001), vol. 4416. International Society for Optics and Photonics; 2001. p. 260–3.
[52] Dayton D, Gonglewski J, Pierson B, Spielbusch B. Atmospheric structure function measurements with a Shack-Hartmann wave-front sensor. Opt Lett 1992;17:1737–9.
[53] Ricklin JC, Davidson FM. Atmospheric turbulence effects on a partially coherent Gaussian beam: implications for free-space laser communication. J Opt Soc Am A 2002;19:1794–802.
[54] Booth MJ. Adaptive optics in microscopy. Philos Trans R Soc Lond Math Phys Eng Sci 2007;365:2829–43.
[55] Cha JW, Ballesta J, So PTC. Shack-hartmann wavefront-sensor-based adaptive optics system for multiphoton microscopy. J Biomed Opt 2010;15:046022–046022–10.
[56] Liang J, Grimm B, Goelz S, Bille JF. Objective measurement of wave aberrations of the human eye with the use of a hartmann-shack wave-front sensor. J Opt Soc Am A 1994;11:1949–57.
[57] Moreno-Barriuso E, Navarro R. Laser ray tracing versus hartmann-shack sensor for measuring optical aberrations in the human eye. J Opt Soc Am A 2000;17:974–85.
[58] Kohnen T, Koch DD, et al. Cataract and refractive surgery. Springer; 2006.
[59] Gerchberg RW. Phase determination from image and diffraction plane pictures in the electron microscope. Optik 1971;34:275–84.
[60] Gerchberg RW, Saxton WO. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik (Jena) 1972;35:237.
[61] Miao J, Charalambous P, Kirz J, Sayre D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999;400(6742):342–4.
[62] Zuo JM, Vartanyants I, Gao M, Zhang R, Nagahara LA. Atomic resolution imaging of a carbon nanotube from diffraction intensities. Science 2003;300(5624):1419–21.
[63] Marchesini S, He H, Chapman HN, Hau-Riege SP, Noy A, Howells MR, Weierstall U, Spence JCH. X-ray image reconstruction from a diffraction pattern alone. Phys Rev B 2003;68:140101.
[64] Eisebitt S, Lning J, Schlotter WF, Lrgen M, Hellwig O, Eberhardt W, Sthr J. Lensless imaging of magnetic nanostructures by X-ray spectro-holography. Nature 2004;432:885–8.
[65] Gonsalves RA, Chidlaw R. Wavefront sensing by phase retrieval. In: Applications of Digital Image Processing III, vol. 207. International Society for Optics and Photonics; 1979. p. 32–9.
[66] Guyon O. Limits of adaptive optics for high-contrast imaging. ApJ 2005;629(1):592.
[67] Pedrini G, Osten W, Zhang Y. Wave-front reconstruction from a sequence of interferograms recorded at different planes. Opt Lett 2005;30(8):833–5.
[68] Anand A, Pedrini G, Osten W, Almoro P. Wavefront sensing with random amplitude mask and phase retrieval. Opt Lett 2007;32(11):1584–6.
[69] Almoro PF, Pedrini G, Gundu PN, Osten W, Hanson SG. Phase microscopy of technical and biological samples through random phase modulation with a diffuser. Opt Lett 2010;35(7):1028–30.
[70] Mudanyali O, Tseng D, Oh C, Serhan OI, Sencan I, Bishara W, Oztoprak C, Seo S, Khademhosseini B, Ozcan A. Compact, light-weight and cost-effective microscope based on lensless incoherent holography for telemedicine applications. Lab Chip 2010;10(11):1417–28.
[71] Tseng D, Mudanyali O, Oztoprak C, Serhan OI, Sencan I, Yaglidere O, Ozcan A. Lensfree microscopy on a cellphone. Lab Chip 2010;10(14):1787–92.
[72] Wackerman CC, Yagle AE. Use of fourier domain real-plane zeros to overcome a phase retrieval stagnation. J Opt Soc Am A 1991;8(12):1898–904.
[73] Lu G, Zhang Z, Yu FTS, Tanone A. Pendulum iterative algorithm for phase retrieval from modulus data. Opt Eng 1994;33(2):548–55.
[74] Takajo H, Takahashi T, Kawanami H, Ueda R. Numerical investigation of the iterative phase-retrieval stagnation problem: territories of convergence objects and holes in their boundaries. J Opt Soc Am A 1997;14(12):3175–87.
[75] Misell DL. A method for the solution of the phase problem in electron microscopy. J Phys D: Appl Phys 1973;6(1):L6.
[76] Allen LJ, Oxley MP. Phase retrieval from series of images obtained by defocus variation. Opt Commu 2001;199:65–75.
[77] Zhang Y, Pedrini G, Osten W, Tiziani HJ. Whole optical wave field reconstruction from double or multi in-line holograms by phase retrieval algorithm. Opt Express 2003;11(24):3234–41.
[78] Bao P, Zhang F, Pedrini G, Osten W. Phase retrieval using multiple illumination wavelengths. Opt Lett 2008;33(4):309–11.
[79] Zhang F, Pedrini G, Osten W. Phase retrieval of arbitrary complex-valued fields through aperture-plane modulation. Phys Rev A 2007;75(4):043805.
[80] Fannjiang A, Liao W. Phase retrieval with random phase illumination. J Opt Soc Am A 2012;29(9):1847–59.
[81] Almoro P, Pedrini G, Osten W. Complete wavefront reconstruction using sequential intensity measurements of a volume speckle field. Appl Optics 2006;45(34):8596–605.
[82] Gao P, Pedrini G, Zuo C, Osten W. Phase retrieval using spatially modulated illumination. Opt Lett 2014;39(12):3615.
[83] Bates RHT. Uniqueness of solutions to two-dimensional fourier phase problems for localized and positive images. Computer Vision, Graphics, and Image Processing 1984;25(2):205–17.
[84] Fienup JR, Wackerman CC. Phase-retrieval stagnation problems and solutions. J Opt Soc Am A 1986;3(11):1897–907.
[85] Seldin JH, Fienup JR. Numerical investigation of the uniqueness of phase retrieval. J Opt Soc Am A 1990;7(3):412–27.
[86] Guizar-Sicairos M, Fienup JR. Understanding the twin-image problem in phase retrieval. J Opt Soc Am A 2012;29(11):2367–75.
[87] Fienup JR. Phase retrieval algorithms: a comparison. Appl Optics 1982;21(15):2758–69.
[88] Fienup JR. Reconstruction of an object from the modulus of its Fourier transform. Opt Lett 1978;3(1):27–9.
[89] Bauschke HH, Combettes PL, Luke DR. Hybrid projection-reflection method for phase retrieval. J Opt Soc Am A 2003;20(6):1025–34.
[90] Elser V. Phase retrieval by iterated projections. J Opt Soc Am A 2003;20(1):40–55.
[91] Luke DR. Relaxed averaged alternating reflections for diffraction imaging. Inverse Problems 2005;21(1):37–50.
[92] Oszlányi G, Sütő A. Ab initio structure solution by charge flipping. Acta Crystallogr A 2004;60(2):134–41.
[93] Marchesini S. Invited article: A unified evaluation of iterative projection algorithms for phase retrieval. Rev Sci Instrum 2007;78(1):011301.
[94] Hegerl R, Hoppe W. Dynamische Theorie der Kristallstrukturanalyse durch Elektronenbeugung im inhomogenen Primrstrahlwellenfeld. Berichte der Bunsengesellschaft fr physikalische Chemie 1970;74(11):1148–54.
[95] Faulkner HML, Rodenburg JM. Movable aperture lensless transmission microscopy: A novel phase retrieval algorithm. Phys Rev Lett 2004;93(2):023903.
[96] Faulkner HML, Rodenburg JM. Error tolerance of an iterative phase retrieval algorithm for moveable illumination microscopy. Ultramicroscopy 2005;103(2):153–64.
[97] Guizar-Sicairos M, Fienup JR. Phase retrieval with transverse translation diversity: a nonlinear optimization approach. Opt Express 2008;16(10):7264–78.
[98] Thibault P, Dierolf M, Menzel A, Bunk O, David C, Pfeiffer F. High-resolution scanning x-ray diffraction microscopy. Science 2008;321(5887):379–82.
[99] Maiden AM, Rodenburg JM. An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 2009;109(10):1256–62.
[100] Thibault P, Dierolf M, Bunk O, Menzel A, Pfeiffer F. Probe retrieval in ptychographic coherent diffractive imaging. Ultramicroscopy 2009;109(4):338–43.
[101] Thibault P, Guizar-Sicairos M. Maximum-likelihood refinement for coherent diffractive imaging. New J Phys 2012;14(6):063004.
[102] Maiden A, Johnson D, Li P. Further improvements to the ptychographical iterative engine. Optica 2017;4(7):736–45.
[103] Maiden AM, Humphry MJ, Sarahan MC, Kraus B, Rodenburg JM. An annealing algorithm to correct positioning errors in ptychography. Ultramicroscopy 2012a;120:64–72.
[104] Beckers M, Senkbeil T, Gorniak T, Giewekemeyer K, Salditt T, Rosenhahn A. Drift correction in ptychographic diffractive imaging. Ultramicroscopy 2013;126:44–7.
[105] Zhang F, Peterson I, Vila-Comamala J, Diaz A, Berenguer F, Bean R, Chen B, Menzel A, Robinson IK, Rodenburg JM. Translation position determination in ptychographic coherent diffraction imaging. Opt Express 2013;21(11):13592.
[106] Thibault P, Menzel A. Reconstructing state mixtures from diffraction measurements. Nature 2013;494(7435):68–71.
[107] Batey DJ, Claus D, Rodenburg JM. Information multiplexing in ptychography. Ultramicroscopy 2014;138:13–21.
[108] Clark JN, Huang X, Harder RJ, Robinson IK. Dynamic imaging using ptychography. Phys Rev Lett 2014;112(11):113901.
[109] Karl R, Bevis C, Lopez-Rios R, Reichanadter J, Gardner D, Porter C, Shanblatt E, Tanksalvala M, Mancini GF, Murnane M, Kapteyn H, Adams D. Spatial, spectral, and polarization multiplexed ptychography. Opt Express 2015;23(23):30250.
[110] Maiden AM, Humphry MJ, Zhang F, Rodenburg JM. Superresolution imaging via ptychography. J Opt Soc Am A 2011;28(4):604–12.
[111] Humphry MJ, Kraus B, Hurst AC, Maiden AM, Rodenburg JM. Ptychographic electron microscopy using high-angle dark-field scattering for sub-nanometre resolution imaging. Nat Commun 2012;3:730.
[112] Stockmar M, Cloetens P, Zanette I, Enders B, Dierolf M, Pfeiffer F, Thibault P. Near-field ptychography: phase retrieval for inline holography using a structured illumination. Sci Rep 2013;3(1).
[113] Takahashi Y, Suzuki A, Furutaku S, Yamauchi K, Kohmura Y, Ishikawa T. High--resolution and high-sensitivity phase-contrast imaging by focused hard x-ray ptychography with a spatial filter. Appl Phys Lett 2013;102(9):094102.
[114] Maiden AM, Humphry MJ, Rodenburg JM. Ptychographic transmission microscopy in three dimensions using a multi-slice approach. J Opt Soc Am A 2012b;29(8):1606–14.
[115] Godden TM, Suman R, Humphry MJ, Rodenburg JM, Maiden AM. Ptychographic microscope for three-dimensional imaging. Opt Express 2014;22(10):12513.
[116] Suzuki A, Furutaku S, Shimomura K, Yamauchi K, Kohmura Y, Ishikawa T, Takahashi Y. High-resolution multislice x-ray ptychography of extended thick objects. Phys Rev Lett 2014;112(5).
[117] Shimomura K, Suzuki A, Hirose M, Takahashi Y. Precession x-ray ptychography with multislice approach. Phys Rev B 2015;91(21).
[118] Rodenburg JM, Hurst AC, Cullis AG, Dobson BR, Pfeiffer F, Bunk O, David C, Jefimovs K, Johnson I. Hard-x-ray lensless imaging of extended objects. Phys Rev Lett 2007a;98(3):034801.
[119] Giewekemeyer K, Thibault P, Kalbfleisch S, Beerlink A, Kewish CM, Dierolf M, Pfeiffer F, Salditt T. Quantitative biological imaging by ptychographic x-ray diffraction microscopy. Proceedings of the National Academy of Sciences 2010;107(2):529–34.
[120] Maiden AM, Morrison GR, Kaulich B, Gianoncelli A, Rodenburg JM. Soft X-ray spectromicroscopy using ptychography with randomly phased illumination. Nat Commun 2013;4:1669.
[121] Rodenburg JM, Hurst AC, Cullis AG. Transmission microscopy without lenses for objects of unlimited size. Ultramicroscopy 2007b;107(2-3):227–31.
[122] Hue F, Rodenburg JM, Maiden AM, Sweeney F, Midgley PA. Wave-front phase retrieval in transmission electron microscopy via ptychography. Phys Rev B 2010;82(12).
[123] Hue F, Rodenburg JM, Maiden AM, Midgley PA. Extended ptychography in the transmission electron microscope: Possibilities and limitations. Ultramicroscopy 2011;111(8):1117–23.
[124] Brady GR, Guizar-Sicairos M, Fienup JR. Optical wavefront measurement using phase retrieval with transverse translation diversity. Opt Express 2009;17(2):624–39.
[125] Maiden AM, Rodenburg JM, Humphry MJ. Optical ptychography: a practical implementation with useful resolution. Opt Lett 2010;35(15):2585–7.
[126] Marrison J, Rty L, Marriott P, O’Toole P. Ptychography - a label free, high-contrast imaging technique for live cells using quantitative phase information. Sci Rep 2013;3(1).
[127] Zheng G, Horstmeyer R, Yang C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat Photonics 2013;7(9):739–45.
[128] Ou X, Zheng G, Yang C. Embedded pupil function recovery for Fourier ptychographic microscopy. Opt Express 2014;22(5):4960.
[129] Sun J, Chen Q, Zhang Y, Zuo C. Efficient positional misalignment correction method for Fourier ptychographic microscopy. Biomed Opt Express 2016a;7(4):1336.
[130] Yeh L-H, Dong J, Zhong J, Tian L, Chen M, Tang G, Soltanolkotabi M, Waller L. Experimental robustness of Fourier ptychography phase retrieval algorithms. Opt Express 2015;23(26):33214.
[131] Dong S, Shiradkar R, Nanda P, Zheng G. Spectral multiplexing and coherent-state decomposition in fourier ptychographic imaging. Biomed Opt Express 2014;5(6):1757.
[132] Tian L, Li X, Ramchandran K, Waller L. Multiplexed coded illumination for fourier ptychography with an LED array microscope. Biomed Opt Express 2014;5(7):2376–89.
[133] Sun J, Chen Q, Zhang Y, Zuo C. Sampling criteria for fourier ptychographic microscopy in object space and frequency space. Opt Express 2016b;24(14):15765.
[134] Li P, Batey DJ, Edo TB, Rodenburg JM. Separation of three-dimensional scattering effects in tilt-series fourier ptychography. Ultramicroscopy 2015;158:1–7.
[135] Tian L, Waller L. 3d intensity and phase imaging from light field measurements in an LED array microscope. Optica 2015a;2(2):104.
[136] Horstmeyer R, Chen RY, Ou X, Ames B, Tropp JA, Yang C. Solving ptychography with a convex relaxation. New J Phys 2015;17(5):053044.
[137] Zuo C, Sun J, Chen Q. Adaptive step-size strategy for noise-robust Fourier ptychographic microscopy. Opt Express 2016a;24(18):20724.
[138] Sun J, Zuo C, Zhang L, Chen Q. Resolution-enhanced Fourier ptychographic microscopy based on high-numerical-aperture illuminations. Sci Rep 2017;7(1):1187.
[139] Williams GJ, Quiney HM, Peele AG, Nugent KA. Coherent diffractive imaging and partial coherence. Phys Rev B 2007;75:104102. doi:10.1103/PhysRevB.75.104102.
[140] Teague MR. Irradiance moments: their propagation and use for unique retrieval of phase. J Opt Soc Am 1982;72(9):1199–209.
[141] Teague MR. Deterministic phase retrieval: a green’s function solution. J Opt Soc Am A 1983;73(11):1434–41.
[142] Streibl N. Phase imaging by the transport equation of intensity. Opt Commun 1984;49(1):6–10.
[143] Ichikawa K, Lohmann AW, Takeda M. Phase retrieval based on the irradiance transport equation and the Fourier transform method: experiments. Appl Optics 1988;27(16):3433–6.
[144] Roddier F. Wavefront sensing and the irradiance transport equation. Appl Optics 1990;29(10):1402–3.
[145] Roddier F, Roddier C, Roddier N. Curvature Sensing: A New Wavefront Sensing Method. In: Morris GM, editor. Statistical Optics, vol. 0976. SPIE; 1988. p. 203–9. International Society for Optics and Photonics
[146] Roddier F. Curvature sensing and compensation: a new concept in adaptive optics. Appl Optics 1988;27(7):1223–5.
[147] Roddier NA. Algorithms for wavefront reconstruction out of curvature sensing data. In: Active and Adaptive Optical Systems, vol. 1542. International Society for Optics and Photonics; 1991. p. 120–9.
[148] Roddier C, Roddier F. Wave-front reconstruction from defocused images and the testing of ground-based optical telescopes. J Opt Soc Am A 1993;10(11):2277–87.
[149] Roddier F, Roddier C. Wavefront reconstruction using iterative fourier transforms. Appl Optics 1991;30:1325–7.
[150] Roddier F, Northcott M, Graves JE. A simple low-order adaptive optics system for near-infrared applications. Publ Astron Soc Pac 1991;103(659):131.
[151] Roddier FJ, Anuskiewicz J, Graves JE, Northcott MJ, Roddier CA. Adaptive optics at the university of hawaii i: current performance at the telescope. In: Adaptive Optics in Astronomy, vol. 2201. International Society for Optics and Photonics; 1994. p. 2–9.
[152] Graves JE, Northcott MJ, Roddier FJ, Roddier CA, Close LM. First light for hokupa’a: 36-element curvature AO system at UH. In: Adaptive Optical System Technologies, vol. 3353. International Society for Optics and Photonics; 1998. p. 34–43.
[153] Arsenault R, Alonso J, Bonnet H, Brynnel J, Delabre B, Donaldson R, Dupuy C, Fedrigo E, Farinato J, Hubin NN, et al. Macao-vlti: an adaptive optics system for the eso interferometer. In: Adaptive Optical System Technologies II, vol. 4839. International Society for Optics and Photonics; 2003. p. 174–85.
[154] Hayano Y, Takami H, Guyon O, Oya S, Hattori M, Saito Y, Watanabe M, Murakami N, Minowa Y, Ito M, et al. Current status of the laser guide star adaptive optic system for subaru telescope. In: Adaptive Optics Systems, vol. 7015. International Society for Optics and Photonics; 2008. p. 701510.
[155] Gureyev TE, Roberts A, Nugent KA. Partially coherent fields, the transport-of-intensity equation, and phase uniqueness. J Opt Soc Am A, JOSA A 1995a;12(9):1942–6.
[156] Gureyev TE, Roberts A, Nugent KA. Phase retrieval with the transport-of-intensity equation: matrix solution with use of Zernike polynomials. J Opt Soc Am A 1995b;12(9):1932–41.
[157] Gureyev TE, Nugent KA. Phase retrieval with the transport-of-intensity equation. II. orthogonal series solution for nonuniform illumination. J Opt Soc Am A 1996;13(8):1670–82.
[158] Gureyev TE, Nugent KA. Rapid quantitative phase imaging using the transport of intensity equation. Opt Commun 1997;133(1):339–46.
[159] Paganin D, Nugent KA. Noninterferometric phase imaging with partially coherent light. Phys Rev Lett 1998;80(12):2586.
[160] Snigirev A, Snigireva I, Kohn V, Kuznetsov S, Schelokov I. On the possibilities of x-ray phase contrast microimaging by coherent high-energy synchrotron radiation. Rev Sci Instrum 1995;66(12):5486–92.
[161] Nugent KA, Gureyev TE, Cookson DF, Paganin D, Barnea Z. Quantitative phase imaging using hard x rays. Phy Rev Lett 1996;77:2961.
[162] Wilkins SW, Gureyev TE, Gao D, Pogany A, Stevenson AW. Phase-contrast imaging using polychromatic hard x-rays. Nature 1996;384(6607):335.
[163] Cloetens P, Ludwig W, Baruchel J, Van Dyck D, Van Landuyt J, Guigay JP, Schlenker M. Holotomography: Quantitative phase tomography with micrometer resolution using hard synchrotron radiation x rays. Appl Phys Lett 1999;75(19):2912–14.
[164] Allman BE, McMahon PJ, Nugent KA, Paganin D, Jacobson DL, Arif M, Werner SA. Phase radiography with neutrons. Nature 2000;408:158.
[165] McMahon PJ, Allman BE, Jacobson DL, Arif M, Werner SA, Nugent KA. Quantitative phase radiography with polychromatic neutrons. Phys Rev Lett 2003;91(14):145502.
[166] Bajt S, Barty A, Nugent KA, McCartney M, Wall M, Paganin D. Quantitative phase-sensitive imaging in a transmission electron microscope. Ultramicroscopy 2000;83(1-2):67–73.
[167] Allen LJ, Faulkner HML, Nugent KA, Oxley MP, Paganin D. Phase retrieval from images in the presence of first-order vortices. Phys Rev E 2001a;63(3):037602.
[168] Allen LJ, Faulkner HML, Oxley MP, Paganin D. Phase retrieval and aberration correction in the presence of vortices in high-resolution transmission electron microscopy. Ultramicroscopy 2001b;88(2):85–97.
[169] McMahon PJ, Barone-Nugent ED, Allman BE, Nugent KA. Quantitative phase-amplitude microscopy II: differential interference contrast imaging for biological TEM. J Microsc 2002;206(3):204–8.
[170] Volkov VV, Zhu Y. Phase imaging and nanoscale currents in phase objects imaged with fast electrons. Phys Rev Lett 2003;91(4):043904.
[171] Beleggia M, Schofield MA, Volkov VV, Zhu Y. On the transport of intensity technique for phase retrieval. Ultramicroscopy 2004;102(1):37–49.
[172] Volkov VV, Zhu Y. Lorentz phase microscopy of magnetic materials. Ultramicroscopy 2004;98(2):271–81.
[173] McVitie S, Cushley M. Quantitative fresnel lorentz microscopy and the transport of intensity equation. Ultramicroscopy 2006;106(4-5):423–31.
[174] Petersen TC, Keast VJ, Paganin DM. Quantitative TEM-based phase retrieval of mgo nano-cubes using the transport of intensity equation. Ultramicroscopy 2008;108(9):805–15.
[175] Barty A, Nugent KA, Paganin D, Roberts A. Quantitative optical phase microscopy. Opt Lett 1998;23(11):817–19.
[176] Barty A, Nugent KA, Roberts A, Paganin D. Quantitative phase tomography. Opt Commun 2000;175(4-6):329–36.
[177] Barone-Nugent ED, Barty A, Nugent KA. Quantitative phase-amplitude microscopy I: optical microscopy. J Microsc 2002;206(3):194–203.
[178] Streibl N. Three-dimensional imaging by a microscope. J Opt Soc Am A, JOSAA 1985;2(2):121–7.
[179] Sheppard CJR. Three-dimensional phase imaging with the intensity transport equation. Appl Optics 2002;41:5951–5.
[180] Curl CL, Bellair CJ, Harris PJ, Allman BE, Roberts A, Nugent KA, Delbridge LMD. Quantitative phase microscopy: a new tool for investigating the structure and function of unstained live cells. Clin Exp Pharmacol Physiol 2004;31(12):896–901.
[181] Curl CL, Bellair CJ, Harris PJ, Allman BE, Roberts A, Nugent KA, Delbridge LMD. Single cell volume measurement by quantitative phase microscopy (QPM): a case study of erythrocyte morphology. Cell Physiol Biochem 2006;17(5-6):193–200.
[182] Ross GJ, Bigelow AW, Randers-Pehrson G, Peng CC, Brenner DJ. Phase-based cell imaging techniques for microbeam irradiations. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At 2005;241(1):387–91.
[183] Dragomir NM, Goh XM, Curl CL, Delbridge LMD, Roberts A. Quantitative polarized phase microscopy for birefringence imaging. Opt Express 2007;15(26):17690–8.
[184] Roberts A, Ampem-Lassen E, Barty A, Nugent KA, Baxter GW, Dragomir NM, Huntington ST. Refractive-index profiling of optical fibers with axial symmetry by use of quantitative phase microscopy. Opt Lett 2002;27(23):2061–3.
[185] Ampem-Lassen E, Huntington ST, Dragomir NM, Nugent KA, Roberts A. Refractive index profiling of axially symmetric optical fibers: a new technique. Opt Express 2005;13(9):3277–82.
[186] Dorrer C, Zuegel JD. Optical testing using the transport-of-intensity equation. Opt Express 2007;15(12):7165–75.
[187] Darudi A, Shomali R, Tavassoly MT. Determination of the refractive index profile of a symmetric fiber preform by the transport of intensity equation. Opt Laser Technol 2008;40(6):850–3.
[188] Kou SS, Waller L, Barbastathis G, Sheppard CJR. Transport-of-intensity approach to differential interference contrast (TI-DIC) microscopy for quantitative phase imaging. Opt Lett 2010;35(3):447–9.
[189] Waller L, Tian L, Barbastathis G. Transport of intensity phase-amplitude imaging with higher order intensity derivatives. Opt Express 2010a;18(12):12552–61.
[190] Waller L, Luo Y, Yang SY, Barbastathis G. Transport of intensity phase imaging in a volume holographic microscope. Opt Lett 2010b;35(17):2961–3.
[191] Waller L, Kou SS, Sheppard CJR, Barbastathis G. Phase from chromatic aberrations. Opt Express 2010c;18(22):22817–25.
[192] Kou SS, Waller L, Barbastathis G, Marquet P, Depeursinge C, Sheppard CJR. Quantitative phase restoration by direct inversion using the optical transfer function. Opt Lett 2011;36(14):2671–3.
[193] Almoro PF, Waller L, Agour M, Falldorf C, Pedrini G, Osten W, Hanson SG. Enhanced deterministic phase retrieval using a partially developed speckle field. Opt Lett 2012;37(11):2088–90.
[194] Gorthi SS, Schonbrun E. Phase imaging flow cytometry using a focus-stack collecting microscope. Opt Lett 2012;37:707–9.
[195] Waller L, Tsang M, Ponda S, Yang SY, Barbastathis G. Phase and amplitude imaging from noisy images by Kalman filtering. Opt Express 2011;19(3):2805–15.
[196] Xue B, Zheng S, Cui L, Bai X, Zhou F. Transport of intensity phase imaging from multiple intensities measured in unequally-spaced planes. Opt Express 2011;19(21):20244–50.
[197] Bie R, Yuan X-H, Zhao M, Zhang L. Method for estimating the axial intensity derivative in the TIE with higher order intensity derivatives and noise suppression. Opt Express 2012;20(7):8186–91.
[198] Zheng S, Xue B, Xue W, Bai X, Zhou F. Transport of intensity phase imaging from multiple noisy intensities measured in unequally-spaced planes. Opt Express 2012;20(2):972–85.
[199] Martinez-Carranza J, Falaggis K, Kozacki T. Optimum measurement criteria for the axial derivative intensity used in transport of intensity-equation-based solvers. Opt Lett 2014a;39(2):182–5.
[200] Falaggis K, Kozacki T, Kujawinska M. Optimum plane selection criteria for single-beam phase retrieval techniques based on the contrast transfer function. Opt Lett 2014;39(1):30–3.
[201] Zuo C, Chen Q, Asundi A. Boundary-artifact-free phase retrieval with the transport of intensity equation: fast solution with use of discrete cosine transform. Opt Express 2014a;22(8):9220.
[202] Zuo C, Chen Q, Li H, Qu W, Asundi A. Boundary-artifact-free phase retrieval with the transport of intensity equation II: applications to microlens characterization. Opt Express 2014b;22(15):18310.
[203] Huang L, Zuo C, Idir M, Qu W, Asundi A. Phase retrieval with the transport-of-intensity equation in an arbitrarily shaped aperture by iterative discrete cosine transforms. Opt Lett 2015;40(9):1976.
[204] Zuo C, Chen Q, Huang L, Asundi A. Phase discrepancy analysis and compensation for fast Fourier transform based solution of the transport of intensity equation. Opt Express 2014c;22(14):17172.
[205] Zuo C, Chen Q, Yu Y, Asundi A. Transport-of-intensity phase imaging using Savitzky-Golay differentiation filter - theory and applications. Opt Express 2013a;21(5):5346–62.
[206] Sun J, Zuo C, Chen Q. Iterative optimum frequency combination method for high efficiency phase imaging of absorptive objects based on phase transfer function. Opt Express 2015;23(21):28031.
[207] Zuo C, Chen Q, Asundi A. Light field moment imaging: comment. Opt Lett 2014d;39(3):654.
[208] Zuo C, Chen Q, Tian L, Waller L, Asundi A. Transport of intensity phase retrieval and computational imaging for partially coherent fields: The phase space perspective. Opt Lasers Eng 2015a;71:20–32.
[209] Zuo C, Sun J, Li J, Zhang J, Asundi A, Chen Q. High-resolution transport-of-intensity quantitative phase microscopy with annular illumination. Sci Rep 2017;7(1):7654.
[210] Li J, Chen Q, Zhang J, Zhang Y, Lu L, Zuo C. Efficient quantitative phase microscopy using programmable annular LED illumination. Biomed Opt Express 2017a;8(10):4687–705.
[211] Li J, Chen Q, Sun J, Zhang J, Pan X, Zuo C. Optimal illumination pattern for transport-of-intensity quantitative phase microscopy. Opt Express 2018a;26(21):27599–614.
[212] Zuo C, Sun J, Zhang J, Hu Y, Chen Q. Lensless phase microscopy and diffraction tomography with multi-angle and multi-wavelength illuminations using a LED matrix. Opt Express 2015b;23(11):14314–28.
[213] Li J, Chen Q, Zhang J, Zhang Z, Zhang Y, Zuo C. Optical diffraction tomography microscopy with transport of intensity equation using a light-emitting diode array. Opt Lasers Eng 2017b;95:26–34.
[214] Li J, Chen Q, Sun J, Zhang J, Ding J, Zuo C. Three-dimensional tomographic microscopy technique with multi-frequency combination with partially coherent illuminations. Biomed Opt Express 2018b;9(6):2526–42.
[215] Li J, Chen Q, Sun J, Zhang J, Zuo C. Multimodal computational microscopy based on transport of intensity equation. J Biomed Opt 2016;21(12):126003.
[216] Zuo C, Chen Q, Qu W, Asundi A. Noninterferometric single-shot quantitative phase microscopy. Opt Lett 2013b;38(18):3538.
[217] Zuo C, Chen Q, Qu W, Asundi A. High-speed transport-of-intensity phase microscopy with an electrically tunable lens. Opt Express 2013c;21(20):24060