Результаты тестирования программы компьютерной томографии
vkUtility/Science/CTomo

Автор: Виктор Кон (http://kohnvict.ucoz.ru/main.htm). Только для посвященных.

Введение в проблему

Метод томографии состоит в том, чтобы получить внутреннее распределение плотности сечения объекта по набору проекций, измеренных под разными углами, в каждой из которых записана интегральная вдоль луча плотность. Метод является неразрушающим и получил исключительно широкое распространение в медицине. Авторы метода даже получили Нобелевскую премию по физиологии и медицине.

Но он также широко используется в физике для диагностики различных материалов. Существует несколько алгоритмов реализации метода. Наиболее распространены метод FBP (filtered back projection) и алгебраический метод. Все методы томографии давно и хорошо описаны в книге

Avinash C. Kak, M. Slaney "Principles of Computerized Tomographic Imaging", IEEE, 1988

По данным сайта Google Академии эта книга на май 2016 года цитировалась 6832 раза. В свое время книгу в электронном виде можно было скачать в интернете, что я и сделал. Правда я потерял ссылку на скачивание и пока не могу ее найти. В 2005 году меня попросили написать свою программу томографии, и я, как примерный пионер, ее сделал. Одновременно я записал небольшой pdf файл о программе, в котором кратко изложил основы метода FBP и детали программной реализации. Вот ссылка на этот файл .

В то время программа так и не была использована и работа оказалась невостребованной. Несколько лет назад я переписал программу под другой набор данных в виде tiff файлов и программа использовалась. Сейчас я решил включить ее в большой набор программ vkUtility, и заодно оптимизировать как методы работы, так и внешний вид, а также протестировать на разных моделях.

Описание метода тестирования и первый пример

Самый лучший способ проверки правильности работы программы -- это использование модельных объектов, структура которых известна. Этот способ предполагает на первом этапе расчет экспериментальных проекций от известного объекта. На втором этапе проекции используются для восстановления структуры объекта с последующим сравнением результата реконструкции с оригиналом. Именно сравнение с оригиналом позволяет понять насколько правильно работает программа.

В качестве модельного объекта я взял картинку острова в океане, точнее фотографию из космоса, которая показана на сайте go2life.net. Вот ссылка на картинку . С помощью программы FastStone Image Viewer я превратил ее в серую, вырезал фрагмент размером 512*512 пикселей, и затем уже с помощью собственной ACL программы сделал клип в виде круга, за пределами которого был просто черный фон.

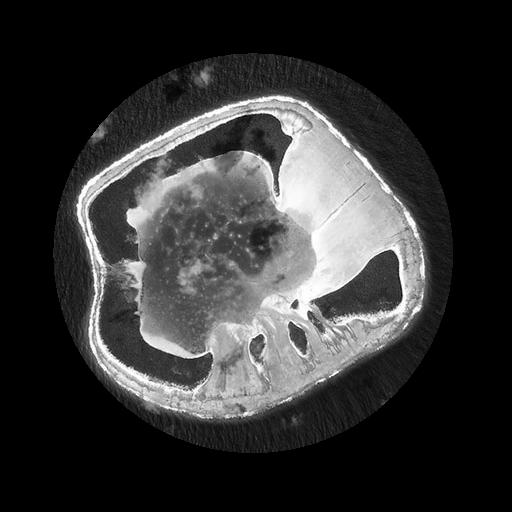
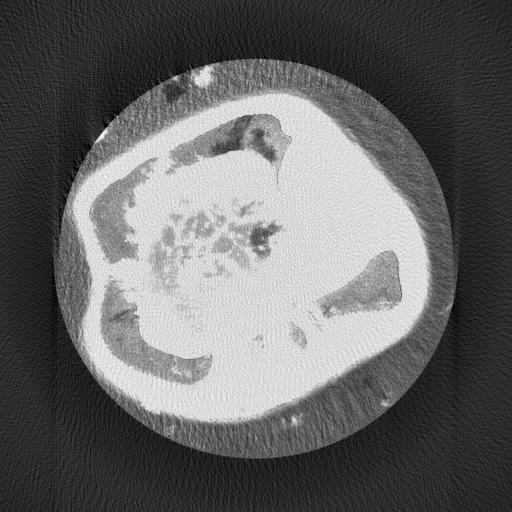
         Рис. 1. Тест с картинкой "белое на черном" с круглой внешней границей.

В результате получилась картинка, показанная выше слева. Картинка может быть развернута в матрицу чисел в интервале от 0 (черный цвет) до 255 (белый цвет), которым я придаю смысл плотности объекта. То есть у меня круглый объект, за пределами которого плотность равна нулю, а внутри него она неравномерно распределена. Проекцию получаем суммированием всех столбцов матрицы. Если матрица имеет размер D*D, где D=512, то проекция имеет D точек, в каждой из которых записана сумма плотностей всех точек столбца.

Далее надо учесть коэффициент поглощения рентгеновских лучей на плотности материала. Тут могут быть варианты. Я ввел параметр M и поставил ему в соответствие максимальное значение произведения коэффициента поглощения на толщину объекта, то есть если бы во всех D точках плотность была 255. Соответственно каждую точку проекции надо умножить на коэффициент -M/(D*255) и вычислить экспоненту. При этом в тех точках проекции, где материала не было совсем, в сумме останется чистый ноль, а экспонента будет равна 1. А там, где материал был, будут числа меньше 1. До нуля не дойдет, но могут быть и маленькие числа.

Так как детекторы обычно записывают свои данные в картинки формата tiff как двухбайтовые целые числа без знака, то максимальное число, которое можно записать равно 65535. Чтобы контраст был высоким я умножил все числа проекции на 65000. Затем картинка внутри круга поворачивалась на заданный угол и расчет проекции повторялся таким же способом. Крутить надо на 180 градусов, а число проекций может быть любым. Для уменьшения времени расчета я для начала задал число проекций N = 180, то есть с шагом один градус.

Программа расчета проекций каждую проекцию записывала в отдельный файл формата tiff так, как делают детекторы, то есть она записала 180 файлов с номерами от 000 до 179. На этом этап моделирования экспериментальных данных закончился. Программа, которая это делает, не является программой томографии. Она написана отдельно и не имеет нужного интерфейса с пользователем.

На следующем этапе запускалась сама программа томографии, которая и тестировалась. Она сделана так, что имеет три независимых модуля расчета. Первый модуль вычисляет синограммы для всех сечений трехмерного объекта по высоте, если объект имеет высоту в направлении оси вращения. Синограмма -- это матрица размерности D*N, в которой все проекции заданного сечения лежат как бы одна над другой. То есть программа выбирает из каждого файла двумерной проекции (если объект имеет высоту) одну строку на заданной высоте, и записывает ее в строку синограммы с вертикальной координатой, соответствующей углу проекции. Эту матрицу она записывает в файл, но одновременно определяет минимальное и максимальное значения матрицы. Их она записывает в другой текстовый файл с названием minmax.txt.

Эта операция выполняется относительно быстро, и ее необходимо выделить для того, чтобы определить самое максимальное значения на всех синограммах. На втором этапе расчета это максимальное значение надо указать в форме ввода входных данных. Правильное задание этого значения гарантирует получение минимального фона на томограмме в тех местах, где нет материала. Программа вычисляет логарифм максимального значения и потом она вычитает из этого значения логарифм всех чисел синограммы. Соответственно, для максимального значения разница будет равна нулю.

Результат расчета по программе томографии показан на картинке выше справа. Программа получает результат в виде матрицы чисел, которая затем конвертируется в jpg картинку с линейной шкалой между минимальным (черный цвет) и максимальным (белый цвет) значениями.  При этом делается небольшая дополнительная оптимизация. Оказалось, что минимум и максимум значений в файле topo001.dat, по которому строится картинка, равны -0.35e-3 и 2.55e-3 при M=1. То есть это очень маленькие значения, что и не удивительно, и, кроме того, минимум меньше нуля, что является ошибкой метода, так как плотность материала не может быть отрицательной. Оптимизация состоит в том, что отрицательные значения заменяются на ноль, что делает картинку более разумной.

Интересно, что фон на томограмме оказался не черный, темный океан за пределами острова оказался довольно светлым, а территория самого острова оказалась за пределами динамического диапазона изображения. То есть мелкие детали светлого изображения не различаются. Первоначально я делал расчет с M=8 и максимальным значением 65000. Затем я повторил расчет с M=1, а затем поменял и максимальное значение на 32500. Топограмма при этом никак не изменилась, а вот синограмма изменилась. Ниже показаны две синограммы для M=8 (слева) и M=1 (справа).    

        Рис. 2. Синограммы для случая рисунка 1 с разными значениями M=8 (слева) и M=1 (справа)

Сразу видно, что левая картинка оказалась недоэкспонированной, то есть коэффициент поглощения был взят очень большим и данные синограммы дают очень маленькие числа во всех точках проекции, где есть объект. Очевидно, что такая картинка получается из-за экспоненциального характера ослабления интенсивности рентгеновских лучей. Экспонента сначала убывает очень быстро, а потом она находится около нуля и картинка с линейной шкалой ничего не различает. Но числа, по которым она записана точные, и при вычислении логарифма информация не теряется. Поэтому на точность реконструкции это не отражается. Изменение максимального значения на 32500, то есть на середину интервала тоже никак не влияет на томограмму. Результат оказался очень устойчивым к изменению параметров.

Другим интересным наблюдением является то, что томограмма намного лучше восстанавливается в областях, где плотность находится вблизи минимума, и очень плохо -- в областях с плотностью вблизи максимума. Чтобы это проверить, я просто превратил картинку в негатив, снова используя программу FastStone Image Viewer, и затем повторил всю процедуру приготовления экспериментальных данных и их реконструкции. При этом было задано M=1, максимум 32500 и обнуление отрицательных значений, теперь это просто зашито в программе.

Результат показан на двух картинках ниже. Слева оригинал, справа -- реконструкция. В целом надо признать, что закономерность подтверждается. Области с высокой плотностью материала очень сильно усредняются, в то время как области с низкой плотностью показывают очень тонкие детали распределения плотности. На томограмме второго случая хорошо видны те детали изображения, которые совершенно не видны на томограмме первого случая, и наоборот. Не очень понятно почему это происходит и как это можно использовать.

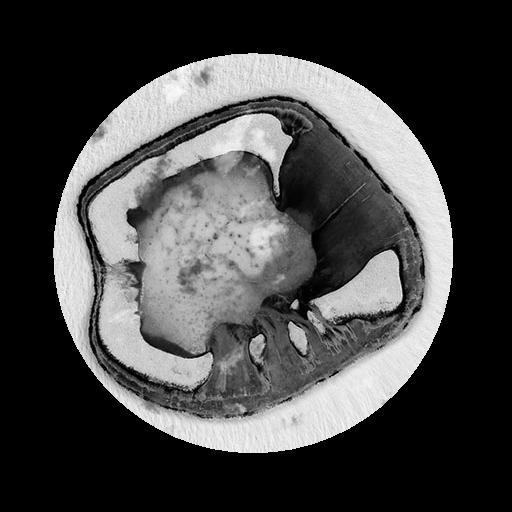
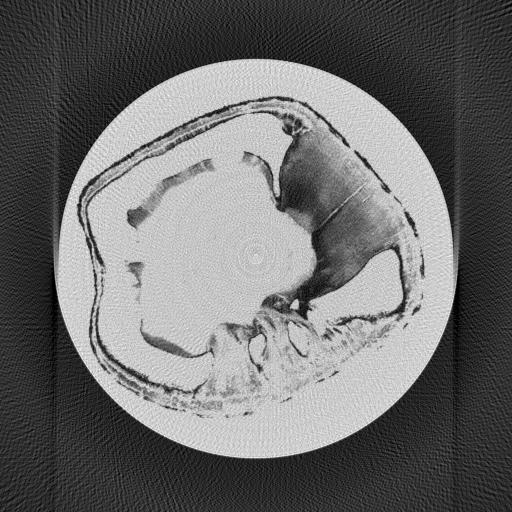
        Рис. 3. Тест с картинкой "черное на белом" с круглой внешней границей.

Можно сказать даже больше. Если рассмотреть интервал от минимума до максимума плотности, то реконструкция хорошо восстанавливает только нижнюю половину этого интервала, в то время как верхняя половина только показывает границы своей области, но внутренняя структура никак не восстанавливается. Интересно, что на второй томограмме в центре стали заметны кольцевые артефакты, присущие методу обратного проектирования. Но намного более сильным недостатком является полное отсутствие деталей изображения в центральной части картинки. Складывается такое ощущение, что области высокой плотности размазываются по всей томограмме, увеличивая плотность тех участков, в которых она низкая, а также делая фон более ярким, чем он должен быть.  

Проверка различных моделей

В прошлой секции я зафиксировал проблему, которая, надо сказать, оказалась для меня неожиданной. Исследование проблемы можно продолжать в разных направлениях. Первое направление очевидно -- это увеличивать число точек проекции и число проекций. Второе направление -- при сохранении параметров рассмотреть различные модели объектов. Второе направление в каком-то смысле более интересно, и я начну с него.

Вот на этом сайте с 2006 года стоит учебная программа по использованию метода CT, написанная на языке Java. Надо сказать, что я сам первую версию своей программы начал делать в 2005 году, а данную программу нашел как только она появилась. В ней рассматривается медицинский фантом, показывающий упрощенную форму мозга. Я нашел аналогичную картинку в интернете, привел ее к размеру 512*512, и затем приготовил проекции и провел реконструкцию по своей программе. В этом случае клип не использовался. Исходная модель и результат реконструкции показаны на рисунках под этим текстом слева и справа. Использовалось значение M=1 и максимум 32500.  

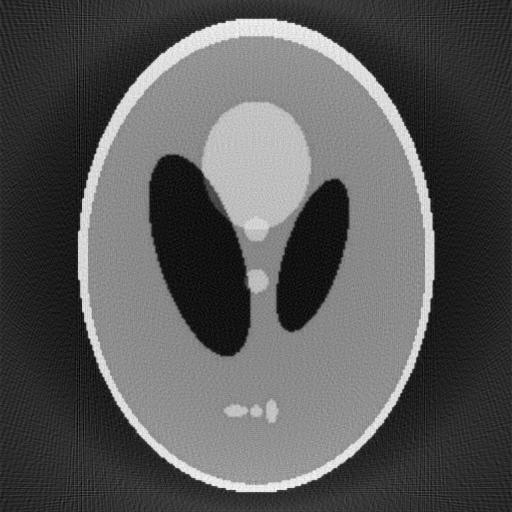
         Рис. 4. Тест с медицинским фантомом.

В целом можно сказать, что результат удовлетворительный. Все контуры объектов восстанавливаются очень хорошо, даже ступеньки, связанные с большой величиной пиксела картинки. И в то же время можно заметить тот же самый дефект, что и выше, а именно, контраст, то есть цвет различных областей получился другим. Видно, что белый контур не является белым, он светлосерый. С другой стороны, серые области внутри контура оказались более светлыми. И только черный цвет остался черным.

Надо сказать, что исправить картинку путем изменения яркости и контраста так, чтобы она совпала с оригиналом, не получится, хотя бы потому, что на картинке справа верхний светлый круг почти равен по цвету контуру, а в оригинале это не так. Интересно сравнить гистограммы картинок. Их можно получить с помощью программы ImageJ. Они показаны на картинках ниже

                 
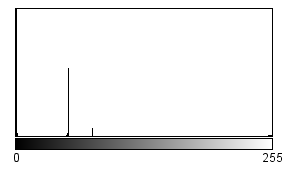
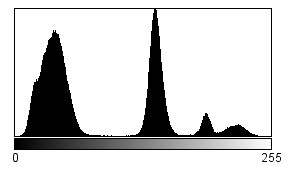
         Рис. 5. Гистограммы теста с медицинским фантомом

Гистограммы никак не учитывают контуры объектов, а только указывают сколько точек каждого цвета есть на картинке. На исходной картинке всего 4 цвета, причем пики черного и белого даже сложно заметить. На картинке, полученной в результате реконструкции, тоже 4 пика. Но они смещены по цветности и имеют довольно большую ширину. Нет ни черного, ни белого, есть темный и светлый, а между ними еще два светлых пика.

И все же реконструкция показывает наличие объектов различной плотности, их границы, а точность воспроизведения самих значений плотности -- это очень сложный вопрос. Я пока не понимаю как вообще возможно это получить.

Интересно проверить модель с минимумом цветов, но с большим числом резких границ мелких объектов. Такой моделью может быть текст в круге. Результаты тестирования такой модели показаны на картинке внизу этого текста. Снова белый круг дает характерные артефакты фона, которые уже получались выше на рисунке 3. Текст вполне читается, даже тонкие линии на буквах видны. Но цвет круга не белый, а цвет фона не черный.

         Рис. 6. Тест с печатным текстом на белом фоне в круге.

Надо сказать, что с точки зрения обнаружения мелких объектов в структуре образца тест можно считать положительным, тем более, что использовалось всего 180 углов. На такой картинке и правильные цвета (белый и черный) можно получить путем увеличения контраста. Такая картинка показана на рисунке 7 слева. При этом сразу видно, что области закрашиваются неоднородно, а именно, в белой области есть черные помехи, а в черной -- белые. Кроме того, есть характерные линии по нижней и верхней границам строк текста.

Интересно сделать реконструкцию такого объекта, используя 360 углов. Это легко выполнимая задача, причем мне показалось, что время счета не слишком сильно увеличилось при увеличении числа углов вдвое. Это легко понять, если знать детали метода. Основное время занимает процедура набора пикселей картинки из вспомогательного массива путем интерполяции. При этом главную роль в формировании времени расчета играет размер картинки, а не число проекций. Результат расчета показан на том же рисунке справа.

 
         Рис. 7. Слева томограмма рисунка 6 с более высоким контрастом, справа -- при использовании 360 проекций.

Сравнивая два результата при разном числе проекций, можно сделать вывод, что увеличение числа проекций делает следующее: (1) сглаживает полосатую структуру как фона, так и объекта, (2) увеличивает контраст, то есть буквы стали более черные, фон стал более светлым. То есть качество инфоормации слегка возросло, но не количество. Картинка дает вполне читаемый текст уже при 180 проекциях. На точной картинке стали более заметны кольцевые артефакты.  

Важным параметром является время расчета томограмм. К сожалению здесь похвататься нечем. Расчет одного сечения размером 512*512 занимает примерно 40 секунд. Я решил сделать тест на размер 1024*360. В качестве образца я выбрал картинку показанную на рисунке 8. В ней всего два цвета: черный и белый, и относительно мелкий текст. Результат реконструкции показан на рисунке 9. Текст четко виден, но фон не булый. Теперь о времени расчета. На ноутбуке Dell (оперативная память 8 гб, процессор Intel Сore-i5-3210M 2.50 Hz) время расчета было 174 сек. То есть примерно в 4 раза больше. Это и не удивительно, так как все время расчета сидит на формировании картинки по точкам методом интеграла по углу от функции, зависящей от угла неявным образом, через зависимость аргумента. При этом я просто интерполирую небольшой массив. И чем больше точек, тем больше время. Число точек как раз увеличивается в 4 раза при увеличении линейного размера в 2 раза. В этом случае использовалась JRE-64, то есть на 64 битный процессор.

Я также провел расчет на ультрабуке Самсунг (оперативная память 4 гб, процессор Intel Сore-i5-2537M 1.40 Hz) и с JRE-32. Время счета было примерно 180 секунд, то есть не намного больше. Получается так, что время даже не зависит от версии JRE. Однако, вот интересный момент. Это время Самсунг показывает при зарядке от сети. А если работать на аккумуляторе, то время возрастает до 270 секунд. Вероятно у процессора Intel Core-i5 есть разные режимы работы. Режим от аккумулятора на Dell я не проверял.

Вообще говоря, время расчета очень большое и есть необходимость как-то его уменьшить. Я просмотрел код процедуры, которая держит все время. Там был тройной цикл, внутри самого внутреннего цикла вычислялись косинус и синус, которые не зависели от первых двух циклов. Достаточно было вычислить эти функции предварительно в массивы и брать значения из массивов, как время расчета сразу уменьшилось в 3 раза. В свое время я об этом не думал, так как одно сечение и так быстро считалось, а на трехмерные объекты я не рассчитывал. Это была ошибка и сейчас она исправлена. Вместо 174 секунд для 1024 точек и 360 проекций я получил 56 секунд.    

 
      Рис. 8. Образец для томографии на 1024 точки.

 
      Рис. 9. Результат томографической реконструкции образца на 1024 точки.