О программировании на ACL. Первые шаги и прогулка по возможностям.
Виктор Кон, . . . 17-04-22, 05-09-23, . . . http://kohnvict.narod.ru
Данная статья имеет своей целью дать первые сведения о возможностях языка программирования ACL выполнять достаточно сложные работы весьма простым способом. Язык базируется на возможностях языка Java, но устроен принципиально другим способом с единственной целью записывать код как можно компактнее, а программировать как можно проще, при этом не теряя способностей делать все, что необходимо. Он совмещает в себе все уровни от примитивного, когда выполняются элементарные операции, до уровня zero-coding, когда весьма сложные программы запускаются как элементарные операции. Есть возможность использовать готовые макросы и создавать новые с нуля и разными способами.
Содержание
01. Введение.
02. Немного о том, как это работает.
03. Взаимодействие программы с пользователем.
04. Делаем новую картинку как фрагмент старой и немного о другом.
05. Делаем новую картинку из числовой матрицы.
06. Научная графика.
07. Анимация.
08. Математические вычисления. С чего все начиналось.
09. Работа с файлами и форматы данных.
10. Архивы файлов. Много в одном и компактно.
11. Работа с текстом. Надо понять что написано.
12. Графика 1. Простой вариант.
13. Графика 2. Сложный вариант.
14. Разные мелочи, важные в работе.
15. И кое-что еще, о чем не говорят.
16. О проблемах распределения и генерации кода ACL.
17. Научная графика и суперкоманды еще раз более подробно.
.
1. ВВЕДЕНИЕ.
Ситуация в мире все время меняется. И особенно сильно в последнее время. И особенно в России. Возникла проблема импортозамещения и опоры на собственные силы во всех областях, включая область цифровых технологий и компьютеризации. Соответственно растет интерес к программированию. Появляются разные курсы обучения программированию с нуля и до профессии с высокой зарплатой. И раньше их было много, а сейчас становится еще больше. Я зарплату не обещаю, но возможно кому-то интересно освоить программирование для ускорения своей работы или творчества, как хобби. Таким людям я могу помочь в том плане, что предложить программу, которая сочетает в себе достаточно высокие возможности программирования с очень простой организацией как самого языка, так и среды разработки программ на нем, которую я сам сделал для себя и которой постоянно пользуюсь.
Увы, человек есть животное стадное, поэтому большинство людей стремится быть как все, и делать то, что делают все. Хорошо это или плохо каждый решает сам для себя. Должен огорчить таких людей, так как у меня не так, как у всех, как раз по другому, как лично мне всегда нравилось. И как раз тем из вас, кому не нравится то, что всем навязывают, как стандарт, я предлагаю попробовать нечто новое. Моя специфика в том, что я давно родился, и начинал программировать когда еще ничего не было и все приходилось делать самому. В то время все так делали, и я так делал. Но, в отличие от других, я все, что делал, сохранял для дальнейшего использования. В результате такой организации работы я накопил очень большой объем кода, который позволяет делать почти все, что нужно лично мне. А мне нужно достаточно много, хотя, конечно, не все на свете. Я ученый, теоретик и мне нужно уметь делать расчеты, создавать и показывать графики, а также анимацию и цветные картинки. Вообще работать с данными.
Сразу скажу чего в моем языке программирования нет. Нет работы с видео, базами данными, точнее огромными базами данных, нет нейро-сетей, то есть искусственного интеллекта и вообще всего того, что появилось в 21-м веке. Это все мне лично не нужно, ни для моей работы, ни для моих интересов. Да и нет времени этим заниматься. Свой язык программирования я придумал 30 лет назад, с тех пор он развивался и сейчас развивается. Но в тех рамках, которые нужны для научной работы и увлечений физика-теоретика. Зато он вполне удобен для тех, кто только начинает программировать и пока еще ничего не знает. Потому что даже самые простые программы, написанные для ваших целей, сразу увеличивают ваши возможности использования компьютера в разы по сравнению с готовыми программами. И это полезно многим, кто не является махровым специалистом в области компьютерных и интернет технологий.
В этой статье я попробую показать как просто и быстро можно написать некоторые программы с помощью моего языка программирования. Удобство моей программы в том, что у нее очень легкий способ вхождения в тему. Практически ничего не надо устанавливать. Просто скачали файл-архив, скопировали папку из архива на компьютер и все, можно работать. И вот как раз первые шаги в такой работе я и попробую объяснить. А также показать некоторые возможности писать программы любой степени сложности.
2. НЕМНОГО О ТОМ, КАК ЭТО РАБОТАЕТ.
Программы пишутся на языке ACL (advanced command language). Это интерпретируемый язык, и для его работы необходим интерпретатор этого языка. Интерпретатор сделан таким образом, что он сам является готовой программой, написанной на языке программирования Java. Для операционной системы компьютера все программы, написанные на языке ACL, являются разными вариантами Java программы, которая сама интерпретируется программой java.exe (в системе Виндовс), которая является частью виртуальной машины (сокращенно JRE) языка программирования Java. Эта виртуальная машина бесплатно поставляется ее разработчиками и она является просто расширением операционной системы. Она работает во всех главных операционных системах.
Интерпретатор ACL сейчас существует в 3-х вариантах. Во-первых, есть старая версия, которая называется vkACL. Эта программа была написана первой. Она имеет много файлов, дает средства для разработки программ и дополнительные возможности в том виде, в каком программа создавалась в самом начале. Программа vkACL имеет свой сайт 
, откуда ее можно скачать. Там же дается архив большого числа базовых программ, представляющих интерес для всех. Эта программа имеет свое собственное окно и большие возможности для работы. Она не только дает средства разработки новых программ на этом языке, но и является удобным навигатором по большому набору уже написанных автором программ. Но эта версия уже не развивается. Она заморожена и нужна только для запуска старых ACL программ.
Во-вторых, есть примерно такая-же программа, но у которой немного другая структура, другое меню окна, меньше файлов и еще больше возможностей. Она отличается от первой версии тем, что некоторые методы программирования в ней работают иначе. По этой причине старые ACL программы она выполнить не сможет, если их не переписать на новый манер. Как раз поэтому старая версия продолжает существовать. Но тем, кто только начинает осваивать язык ACL, лучше сразу начинать со второй версии. Пока ее можно скачать с уже указанного выше сайта, она там стоит в списке первой, но в будущем у нее будет свой сайт. Условно назовем ее ACLm. Буква m от слова modern, то есть современная. В будущем она будет развиваться дальше и иметь новые версии.
В третьих, есть более компактная программа, которая просто исполняет ACL программы без своего окна. Она работает так же, как работали практически все старые программы в системе ДОС. То есть она может взять ACL код и входные данные из файла, проделать работу, записать результаты в файл и совсем не использовать окна Виндовс, как будто их и нет вовсе. Такой вариант программы удобен при использовании автоматической работы в виде набора команд, среди которых есть программы разного происхождения и структуры, написанные на разных языках программирования. Такой вариант также удобен для презентаций, анимаций, лекций и прочей работы без участия пользователя и общения с ним. Условно назовем ее ACLp. Буква p от слова player, то есть проигрыватель.
Автором как языка, так и всех программ-интерпретаторов (далее ПИ), является автор этой статьи. Как уже отмечено, ПИ написана на языке Java, и для ее работы нужен интерпретатор этого языка. Но это уже широко известная техника, на указанном выше сайте написано что и как надо делать. Известно, что язык Java является образцовым объектно ориентированным языком и он особенно хорош для написания очень сложных программ. Интерпретатор как раз и является сложной программой. А мой язык ACL является командным языком и он, наоборот, весьма простой. И, тем не менее, он позволяет сделать на компьютере много всего, но именно благодаря тому факту, что он базируется на сложном и мощном языке Java. Установка первых двух версий программы весьма проста. На сайте все написано. По клавише F11 (или из меню) можно открыть описание программы и прочитать его.
Третья версия тоже записана в zip-архив, но она намного короче и проще. В ней нет окна и она удобна при работе с уже готовыми ACL программами, не содержащими ошибок. Начинать лучше со второй версии. Я повторю тут какие шаги надо выполнить впервые. Выбираете в меню раздел (Program/Open). Откроется строка ввода. Набираете в этой строке такой текст (Intro/1.acl). Нажимаете клавишу [OK]. Откроется редактор текстов, у которого в титульной строке будет написано как раз тот текст, что вы напечатали. Что произошло? Программа создала в папке ПИ новую папку с названием (Intro) и в ней файл в именем 1.acl. Файл еще пустой и программа показывает вам пустой текст этого файла, куда можно писать код на языке ACL. Если вы напишете (или скопируете) в окно редактора какой-то код, то стоит нажать клавишу [F12] как ПИ автоматически запишет код в файл и исполнит его. А потом надо нажать клавишу [F1] и снова появляется окно редактора с кодом программы. Можно еще что-то написать, исправить или изменить. И снова клавиша [F12] все исполнит.
Поясню почему я выбрал именно эти клавиши. Дело в том, что на моем новом ноутбуке только эти клавиши из серии [Fn] нажимаются сразу, а остальные совмещены с клавишами управления работой компьютера и нажимаются только с дополнительной клавишей [fn]. Так появилось относительно недавно, раньше было наоборот. К сожалению, жизнь меняется очень быстро и приходится реагировать.
Со временем у вас появится много файлов с уже написанным кодом. В этом случае тоже можно использовать раздел меню (Program/Open), но если не хотите печатать, то лучше выбрать раздел (Program/Choose) или нажать горячие клавиши [Ctrl]+[C]. После этого остается выбрать файл в менеджере файлов, и он сразу появится в редакторе. Любую разработку новой или изменение старой программы на языке ACL надо делать именно так. Вообще говоря, готовые ACL программы можно запускать и другими способами. Любая ACL программа способна запустить любую другую программу и снова разными способами. Но в этом случае та программа, которая запускается должна переопределить рабочую папку на себя. Иначе будут неприятности с поиском файлов. Об этом более подробно будет написано позднее.
Проще, чем такая система работы с новой программой, я нигде не видел. Да, известно, что у языков Java и Python есть свои среды разработки. Но они очень сложно устанавливаются и очень сложные в работе. А тут все предельно просто. Что касается подсказок, то их нет, а описание языка есть в интернете, вот ссылка , причем с удобной таблицей -- навигатором по всем командам и элементам языка. Для того, чтобы пользоваться всеми возможностями, надо один раз прочитать все описание. А потом достаточно смотреть таблицу и переходить к конкретным разделам этого описания. Как и любой интерпретируемый язык, который записывается просто текстом, язык ACL имеет большой набор базовых команд. Их можно группировать в процедуры, процедуры можно записывать в файл и формировать суперкоманды. На моем сайте есть и другие статьи об указанных программах, языке ACL и методах работы с ним. Адрес сайта указан под заголовком статьи.
Суперкоманды -- это такие команды, которых нет в языке. В старой версии программы их писал сам пользователь в виде процедур, каждую в отдельном файле. Много таких процедур написано мной и они уже готовы к исполнению. Но в этом случае приходится использовать много очень коротких файлов, которые постоянно прочитываются, что замедляет работу программы. В частности суперкоманды в таком виде нельзя использовать в циклах. Они будут изнашивать винчестер частым его использованием. В новой версии суперкоманды записываются в один файл, считываются один раз и остаются в оперативной памяти, так что их можно использовать в циклах, они не тормозят и не изнашивают винчестер.
В любом языке программирования есть средства для операций с данными, это переменные и массивы разных типов. В языке ACL массивы жестко заданы, их всего 4, они различаются типом и размером, определять массивы нельзя. Переменные имеют имена из буквы, буквы и цифры и двух букв. Это тоже массив, но каждый элемент этого массива имеет имя. И это очень просто, поэтому легко усвоить. Такая же ситуация с логикой. Тут тоже не как у всех, но вполне достаточно.
Итак, установить программу, имея компьютер и интернет, можно за несколько минут. Я буду считать, что читатель это уже сделал. И посмотрим примеры как и что можно делать на языке ACL. Написанные ниже примеры будут полезны долгое время, так как описанные ситуации часто используются. Они даже мне полезны, хотя я работаю на своем языке каждый день уже более 18 лет. Именно столько времени существует современная версия на основе Java интерпретатора. До этого язык назывался иначе и интерпретатор был написан на языке Фортран. Хотя язык Java существует с 1995 года, но раньше компьютеры были слабые и он плохо (медленно) работал.
3. ВЗАИМОДЕЙСТВИЕ ПРОГРАММЫ С ПОЛЬЗОВАТЕЛЕМ.
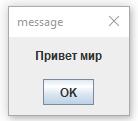Установился шаблон начинать примеры программирования с написания текста (Привет мир) и показа его на экране. На языке ACL это можно сделать большим числом способов. Я покажу как это можно сделать самым удобным способом
#pr Привет мир\E #m [op=win;] \Tp\E
В результате выполнения такого кода программа покажет в центре экрана окошко, которое можно видеть справа от этого текста. Объясню как это работает. При использовании языка программирования ACL в файле можно писать любой текст. ПИ (программа интерпретатор) просматривает этот текст, никак на него не реагируя, пока не увидит символ (#). Этот символ для ПИ является указанием того, что начинается команда. Имя команды может иметь одну, две, три или сколько угодно букв. Но язык так устроен, что для некоторых команд достаточно одной буквы, для других -- двух букв и для всех -- трех букв. Остальные буквы значения не имеют их можно писать только для более легкого понимания команд. Лично я этого не делаю, так как можно быстро привыкнуть понимать все по короткой записи.
Команда pr (print) печатает форматированный текст в текстовый массив. Текст может быть простым, а может содержать команды форматирования, которые начинаются с символа ( \ ). Одна такая команда (\E) обязательна и она указывает на конец записи текста. Сам текст начинается с первого символа, отличного от пробела. Эта команда видит текст (Привет мир) и запоминает его. А вторая команда m (message) показывает на экране текст, который записан в ее аргументе. У этой команды есть не только аргумент (они пишутся в конце записи через пробел), но и текстовый параметр. Значения параметров пишутся в квадратных скобках после имени команды. При этом параметр op имеет значение win, то есть в окне, а аргумент указывает на то, что сам текст надо взять из последней печати.
Важным преимуществом языка ACL является то, что в нем не надо печатать много букв. Значит файлы с кодом программы будут короткими и программа будет быстрее работать. Хотя современные компьютеры тексты обрабатывают быстро, но все равно удобно. Ведь печатать на клавиатуре как раз не быстро. И листать длинные тексты тоже. Экран не резиновый.
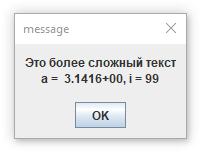Взаимодействие программы с пользователем является весьма важным элементом работы программы, хотя и не основным. Программа вполне могла бы просто считывать числа из файла, делать расчет и результат снова записывать в файл. Именно так работали первые персональные компьютеры, у которых экраны были слабые и показывали плохо. Они и сейчас могут так работать. Но вот если у вас есть очень сложная проблема, то ситуация меняется. Очень редко программы работают без ошибок сразу. Часто поначалу код написан плохо, ПИ не понимает и делает не то. И вот как раз на стадии доработки программы до окончательного рабочего вида такое общение весьма полезно и очень помогает. ПИ должна не только показывать текст, но и значения числовых переменных, комбинацию нового и старого текстов, форматирование строк, специальные символы и много конкретной информации. И команда pr вполне с этим справляется. Рассмотрим более сложный код.
# a=3.14159265; i=99; #pr Это более сложный текст\E #pr \Tp\na =\G a;, i =\I3 i;\n\E #m [op=win;] \Tp\E
Результат выполнения этой программы снова показан на картинке справа. Рассмотрим, что здесь написано. Символ (#) открывает команду. Но на этот раз команда просто определяет значения переменных. Она имеет имя, но его можно не писать. ПИ и так понимает, что команда без имени определяет переменные. Переменной a присвоено значение пи, а переменной i -- значение 99. Потом напечатан текст. А потом еще раз текст, но он весь состоит из команд. Команда \Tp указывает вставить текст, напечатанный предыдущей команды печати. Команда \n означает переход к новой строке. Команда \G печатает числовые значения переменных по общему формату. Он содержит 5 разрядов и показатель степени числа 10, на которое все надо умножить. Команда \I3 указывает напечатать значение переменной i как целое число с тремя разрядами, нули слева заменяются на пробелы. Между командами есть и простой текст типа (a =), (, i =).
Полная информация о возможностях команды pr составить текст любой степени сложности есть в описании языка ACL. Точнее степень сложности все же ограничена, но все, что необходимо, есть, и этого достаточно. А если чего не хватит, то можно сделать. Главное, о чем я заботился, чтобы было удобно записывать и легко читалось. Например Tp == text of print, G == general, I == integer. Ведь все языки программирования сообщают одну и ту же информацию, но различаются степенью удобства реализации задуманного.
Программа должна уметь не только показывать текст, но и картинки. И не только готовые картинки, но и числовые матрицы в виде картинок. И не только стационарно, но и в движении. А еще лучше, когда числовые матрицы быстро вычисляются, преобразуются в картинку, показываются, потом пересчитываются снова, и снова показываются. Так можно даже кино показать. Но не фотографии, а какие-либо процессы, которые программа моделирует вычислениями. И все это тоже делается весьма легко, но все же необходимо двигаться небольшими шагами. Для показа картинок в языке ACL есть команда w. Это одна и наиболее сложных команд. Она имеет много параметров и аргументов и ее возможности весьма высоки. А структура языка такова, что все можно записывать очень просто. Начнем с самого простого, то есть просто показать картинку. Это делает такая команда
#w [op=im; mo=0; sa=0; file=1.jpg;]
Такая команда будет работать только в том случае, если ее запускать из редактора ПИ. Только в этом случае рабочая папка устанавливается автоматически. Если выбрать в меню раздел (Run/File Viewer) и затем нашу программу, то будет выдана ошибка о том, что ПИ не может найти файл. Чтобы избежать такого результата необходимо в явном виде указать в какой папке надо искать файл. То есть написать две команды вот так
#f [op=fold; file=intro;] #w [op=im; mo=0; sa=0; file=1.jpg;]
Программа в таком виде покажет файл (1.jpg) в любом случае, если он реально находится в указанной папке [intro]. Казалось бы, можно было указать полный путь к файлу. Но это тоже не поможет. ПИ так устроена, что даже полный путь к файлу не работает, если рабочая папка не указана. Чтобы полный путь к файлу относительно папки ПИ работал нужно указать папку с названием null, то есть #f [op=fold; file=null;]. В этом случае иногда не только полный путь к файлу относительно папки ПИ работает, но и полный путь на ноутбуке работает, если он начинается с буквы диска. Но об этом позднее.
Результат работы такой программы показан, как обычно, на картинке справа. Окно по умолчанию ставится в середине экрана. Сейчас я хочу объяснить, что даже у этой простой команды много таких свойств, какие отсутствуют в готовых программах. Под картинкой есть системная строка, которая показывает размер картинки в пикселах, текущие координаты курсора и RGB (красный, зеленый, синий) цветовые компоненты пиксела, на который указывает курсор. А сама картинка является кнопкой. Если нажать левую кнопку мышки (кликнуть) когда ее курсор находится над картинкой, то она исчезнет. При этом программа получит информацию о размере картинки (в элементы служебного массива s() с номерами 12 и 13, параметры tw и th), а также о координатах курсора, где был произведен клик (номера 102 и 103, отсчет по вертикали идет сверху). Более того, можно нажать левую клавишу мыши, затем не отпуская ее перенести ее в другое место и там отпустить. В этом случае программа получит координаты как первой (в те же номера), так и второй точки (в номера 104 и 105). Картинку можно закрыть и нажимая клавиатуру. И снова код клавиши или нескольких клавиш будет сообщен в программу.
Это и есть общение с пользователем. Программа может предложить пользователю картинку, на которой нарисовано любое фасонное меню. После выбора пользователя она будет знать что ей делать, то есть что он выбрал. Один тип такого фасонного меню реализован мной в виде суперкоманды. Меню представляет собой длинные клавиши с подписанным текстом и с номером. Выбор можно делать либо кликом мыши, либо по номеру через клавиатуру. Такое меню можно настраивать по размеру и цвету, а после того, как все настроено в суперкоманде, остается только ее указать. Вот как выглядит код меню, показанного на картинке справа.
#e [n=7;] _scom #pr Program, Choose operation|Game rules (read first)|Input Data (main)|Choose variant|Computing|Exit|Comic Sans MS|\E
#e [n=14;] _scom
Здесь уже используются суперкоманды по новой системе. В старой системе суперкоманды имеют имена и запускаются по двум символам (##), после которых идет имя суперкоманды. И такая грамматика была сделана на аппаратном уровне, то есть в Java коде интерпретатора. В новой системе суперкоманды вызываются по номерам и по стандартной процедуре (scom). И этот способ программирования реализован на самом языке ACL, то есть без изменения кода в интерпретаторе. Язык ACL настолько универсален, что позволяет менять себя и программы на лету, даже в процессе работы. Но для суперкоманд таких фокусов не понадобилось. Просто достаточно в самом начале программы один раз определить процедуру
#pro scom #e [b=KY; le=670;] _text @
Процедуры являются важным и мощным средством программирования. Они есть практически во всех языках программирования и были в самом первом языке Фортран. Назначение процедур в том, чтобы записать некоторый код в память, но не исполнять его. То есть процедура определяет некоторый код и присваивает ему имя. И все, больше она ничего не делает. А после того, как этому коду присвоено имя, его можно много раз исполнять в самых разных частях программы. Сама процедура записывается как команда pro, после которой идет через пробел имя процедуры из не более, чем 4-х символов (лучше писать все 4), потом через пробел идет любой код и все это заканчивается символом (@). Я его называю -- жирная точка. А вот исполнение процедуры по имени выполняет команда e, и она тоже может использовать параметры. Наша процедура имеет имя (scom) и она как раз запускает разные суперкоманды по номеру.
Но процедуру можно запускать еще и по условию. Если надо ее запускать всегда, то удобно ставить перед именем символ ( _ ), так наиболее компактно, хотя можно и по другому. Указанная процедура scom будет правильно работать, если пользователь не сделает ошибок. А если сделает, то интерпретатор укажет на ошибку и потребует ее исправить. Однако может возникнуть и еще более неприятная ситуация. По этой причине иногда удобно использовать более сложные процедуры, которые анализируют значения параметров и не дают сделать ошибку. Например, в настоящий момент программа имеет 35 процедур с номерами от 1 до 35. А если указать другой номер, то будут неприятности. Если написать более сложный код, то неприятностей можно избежать. Вот этот код
#pro scom # &$=&; &=(s(7)*(36-s(7)))<1>0; #case 1 #e [b=KY; le=670;] _text # &$=&; #end |
#case 0 #pr Invalid number of pro scom \I9 s(7);\E #e [b=KY; le=670; n=33;] _text #end | # &=&$; @
Рассмотрим что написано выше. В языке ACL переменная (&) имеет уникальное значение. Она является ключом от замка, который открывает двери, то есть позволяет выполниться условию. Процедуры не должны портить значения этой переменной. Поэтому ее значение сначала запоминается в другой переменной, затем ей присваивается значение, равное условию. А после этого записана команда case, аргументом которой является число или значение другой переменной. Эта команда, так же как и команда pro, определяет некоторую часть кода до команды end, которая либо выполнится, либо не выполнится. Условием для выполнения является совпадение значений аргумента команды и переменной (&). При этом значение аргумента команды изменить невозможно, это замок. А вот значение переменной (&) легко изменить, задав любое математическое выражение с использованием операций вычисления максимума и минимума.
При этом надо знать, что элемент массива s(7) эквивалентен параметру (n), только (n) определяется в поле определения параметров (в квадратных скобках), а s(7) -- в математических вычислениях. В записанной конструкции арифметического выражения переменная (&) будет равна 1 если значение s(7) находится в диапазоне от 1 до 35 и будет равна 0 в противном случае. Соответственно при значении 1 выполнится первая процедура внутри скобок case и end, а при значении 0 -- вторая процедура. Первая -- это то, что у нас было раньше. В результате выполнения процедуры значение переменной (&) может измениться и его надо запомнить, чтобы восстановить в конце. А вторая процедура напишет текст, что в программе задан номер процедуры, которая не существует. Я стараюсь писать тексты на английском языке, чтобы иностранцы тоже могли пользоваться. Обычные тексты они переведут на свой язык, а сообщения программы переводить уже сложнее. Также нужно отметить, что вторая процедура сама использует суперкоманду, но с номером 33, который допустим. Эта процедара тоже печатает текст, но она более универсальная, чем #m [op=win;].
Но вернемся к программе, которую мы написали. В ней есть две суперкоманды с номерами 7 и 14. Суперкоманда с номером 7 никакую работу сама не делает. Она просто определяет фиксированный набор параметров для экономии записи текста. Затем надо напечатать текст. Текст разделен символами вертикальной черты, все куски являются названиями клавиш, а последний кусок определяет тип шрифта, которым будет написан текст. И затем просто указываем суперкоманду номер 14, которая все и делает. Заголовки меню можно писать и на русском языке. Но сложность в том, что простой текст переводчики переводят, а вот текст на картинках они не переводят. А английский язык знают больше людей. чем русский. Если писать программу на весь мир, то лучше на английском. А если в этом нет необходимости, то можно и на русском языке писать.
Есть и другие способы писать текст на экране компьютера. Можно писать текст, который появляется на экране, долго стоит и потом исчезает в любое заказанное время. Это могут быть подсказки что дальше делать, подсказки что означают какие-то параметры. Программа может работать во взаимодействии с браузером. Например, я сделал суперкоманду, которая выставляет таблицу из 99 пронумерованных кнопок (матрица 11*9), и клик первой кнопки показывает информацию о том, что делают остальные кнопки в браузере как веб-сайт. Это тоже меню, но из более широкого набора. Суперкоманды удобны тем, что их не надо каждый раз переписывать. Это фактически готовые ACL программы, код которых записан специальным образом, но пользователь даже не обязан его смотреть и знать что там написано.
С другой стороны, это расширение команд языка и примеры готового кода для изучения языка, то есть методов как его можно использовать. Но и в самом языке есть команды, которые могут делать выбор. Так есть команда sel, которая выставляет таблицу кнопок либо с текстом, либо с картинками, в виде прямоугольной матрицы, имеет много параметров, которые настраивают ее внешний вид, и иногда это получается достаточно красиво. В качестве примера я покажу код как раз той суперкоманды с номером 16, которая позволяет выбрать номер варианта из набора от 1 до 99. Вот он
#d 6 i(1) 150 0 0 150 255 150 #col [b=2; le=2; fir=i(1);] # s(3)=1; n=1; #rep 99 #pr \I-2 n;|\E # n=n+1; #end # n=s(3)-1;
#sel [nx=11; ny=9; mo=0; em=1; xs=24; ys=70; col=2; wid=38; hei=28; tsi=24; tfo=3; tki=1;] Choose Variant\E \T1 n\u32;\E
#p [em=0;]
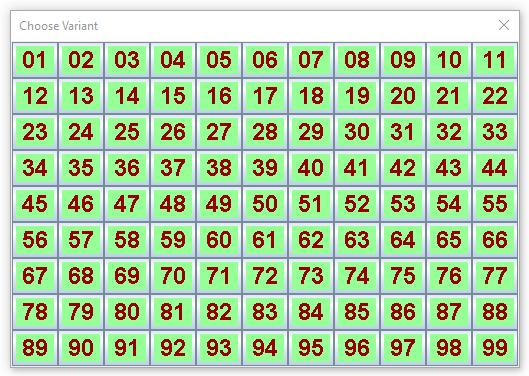В этом коде появились новые команды, я просто укажу что они означают. В контексте изложения конкретного объекта проще понять смысл этих команд. Итак, нам надо задать какими цветами мы будем рисовать кнопки. Для этого надо определить эти цвета. Они определяются по интенсивности красного, зеленого и синего, так называемая rgb модель. Цвета определяет команда #col (color). Ей надо задать три параметра: b (begin), le (length) fir (first). Указано 2, 2 и i(1). Это означает, что будут заданы вариации цвета с номерами, начиная с 2 и всего две. А данные rgb будут взяты из целого массива i(), начиная с первого индекса. И вот как раз команда #d (data) и задает эти цифры. У нее нет параметров, но есть аргументы. Это число значений (6), первый элемент того массива, который определяется i(1), и затем 6 чисел, ровно столько сколько указано. В результате выполнения этой команды будем иметь i(1)=150; i(2)=0; и так далее.
Затем надо напечатать тексты для 99 кнопок. Это можно было бы сделать явно, но это скучно. Поступаем иначе. Элемент служебного массива s(3) всегда определяет первый индекс массива юникодов (текста), в который будет идти печать. Раньше этот вопрос мы не обсуждали, но иногда это важно. Переменная (n) принимает те самые значения, которые будут напечатаны, сначала она равна 1. Команда rep открывает цикл повторений, ее аргумент указывает сколько раз надо повторить. Затем печатаем первое число. Формат \I-2 в отличие от формата \I2 просит ПИ печатать числа в два разряда, но нули слева на пробелы не заменять. Последним символом идет символ вертикальной черты. Это разделитель текстов между кнопками. После того, как напечатали первый номер, надо увеличить значение переменной (n) на единицу. А команда end закрывает цикл. Весь текст перед ней будет повторен столько раз сколько указано.
После того, как цикл закончился, нада определить сколько символов было напечатано. Параметр s(3) играет роль курсора при печати. И при печати каждого символа его значение автоматически увеличивается на единицу. Поэтому вычитая его значение после цикла из первого номера получаем число всех символов. Теперь все готово для применения команды sel. У нее есть параметры. Я просто перечислю что они определяют. nx=11 (число кнопок по горизонтали), ny=9 (то же по вертикали), mo=1 (модификация 1, то есть кнопки текстом), em=1; (продвинутый режим), xs=24; ys=70; (координаты левого верхнего угла окна от левого верхнего угла экрана) col=2; (цвет номер 2, следующий за ним 3 подразумевается), wid=38; hei=28; (размеры кнопки в пикселах по горизонтали и вертикали), tsi=24; (размер текста в пикселах), tfo=3; (тип фонта), tki=1; (вид фонта). Еще у команды есть два аргумента в виде текста. Они форматируются так же, как и при печати, но не печатаются, а просто указываются. Первый текст -- это заголовок, второй -- это имена всех кнопок, разделенные символом вертикальной черты. Команда текста (\T1 n) означает, что текст надо взять из массива символов t(), начиная с первого и до n-го. Это тот самый массив, куда идет вся печать. Как раз командой pr мы его и определяли. ПИ прекрасно понимает этот текст и правильно его исполняет.
Есть еще и другая информация, которую полезно знать пользователю от программы. Например, время работы. Само собой разумеется, что можно смотреть на часы, но иногда все делается очень быстро, а надо сравнить два алгоритма, какой из них быстрее. Если код очень большой, то бывает полезно узнать -- прошла программа заданную точку или нет. Бывает нужно распечатать значения переменных или параметров в каком-то месте. Все это можно делать. Достаточно даже уже указанных команд, но есть и другие. На этом я закончу данный раздел, в следующем разделе рассмотрим как можно делать новые картинки.
4. ДЕЛАЕМ НОВУЮ КАРТИНКУ КАК ФРАГМЕНТ СТАРОЙ И НЕМНОГО О ДРУГОМ.
Люди общаются между собой с помощью текстов и картинок. Это стало особенно удобно в последнее время, когда появились смартфоны с фотоаппаратом и программы типа Вотсап. И раньше все было, но менее удобно. Я сам смартфоном почти не пользуюсь и Вотсапом тоже. Но и сидя дома за ноутбуком получаю много писем по электронной почте, и сам пишу. А также есть социальные сети и сайты, в том числе и мой сайт. Программа не может создавать тексты. Она показывает те тексты, которые ей записал автор. Но если таких текстов очень много и у программы есть код, который анализирует поступающий текст, то она может вполне грамотно отвечать на вопросы. И вот уже появились чат-боты (виртуальные собеседники), которые способны заменить людей в общении.
С картинками ситуация несколько иная. Главное назначение компьютера -- работать с числами, производить вычисления. Как оказалось, числами можно описать не только видимый мир, но и невидимый (виртуальный). а также многомерные пространства с разными свойствами. Но человек не умеет читать числа. Ему надо превратить их в картинки. И есть целая индустрия и много методов превращения набора чисел в картинки. А также есть возможность преобразования уже существующих картинок. В языке ACL все такие работы организованы относительно просто. И как раз об этом и пойдет речь в данной главе. Но сначала несколько слов о структуре языка ACL в целом.
В языке не так уж много команд. Команды делятся на простые и сложные. Простые команды реализуют базовые возможности языка, такие как счет, файлы, условия, циклы. Каждая сложная команда отвечает за целый класс операций определенного типа. Команда w (window) так названа, потому что она результаты своей работы показывает в отдельном окне. И прежде всего это картинки. Любая сложная команда выполняется сложной программой, которая использует входные данные разного типа. Эти данные разделены на параметры и аргументы. Параметры -- это целые числа, элементы массива s(), но многие элементы этого массива имеют имена. Такие параметры сохраняют свое значение до следующего определения. Эти значения можно присваивать в команде расчетов, а можно в специальном блоке сразу после имени любой команды внутри квадратных скобок.
Так сделано просто для удобства чтения программы. Имена параметров помогают понять их назначение. Есть также 4 текстовых параметра, которым присваиваются тексты. Кроме параметров есть аргументы. Они записываются после имени программы и квадратных скобок (если они есть) и прочитываются только один раз при выполнении данной команды. Такие аргументы очень похожи на те, которые имеются в командных языках операционных систем ДОС (Виндовс) и Юникс. Но имеют более сложный вид, так как в них может быть такое же форматирование, как и в команде pr. Команда w имеет много параметров и может иметь аргументы, причем разные в зависимости от значения параметров.
Итак, как показывать картинки мы уже знаем. Но код, который я написал раньше будет работать только если ПИ еще ничего не делала. Более универсальный код такой
#w [op=im; mo=0; file=1.jpg; sa=0; fo=2;]
Здесь в конце добавлены еще два параметра с именами (save) и (formed). Вообще говоря, имена параметров можно писать длинно, если кому так нравится. Просто учитываются только первые три символа или даже меньше для некоторых параметров, которые чаще всего используются.. Дело в том, что кроме типа операции, модификации этого типа и имени файла с картинкой нужно указать что с ней делать. Самое простое -- показать в окне. И если еще ничего не сделано, то параметр sa имеет значение по умолчанию, то есть 0. А если он был определен ранее, то его надо переопределить, иначе будет ошибка.
Фокус в том, что эта команда берет картинку из файла и держит у себя во временной памяти. И она может не только ее показать, но и просто запомнить, не показывая. У ПИ есть шкаф, в котором имеется 100 ящиков, и ПИ может положить картинку в один из этих ящиков на хранение и последующего использования. Такое происходит если параметр (sa) имеет значение от 1 до 100. Еще ПИ может картинку не только показать, но и записать в файл типа (jpg). Это делается при значении (sa=-1). И в этом случае дополнительно нужно указать еще один параметр fo (formed). Он должен содержать имя нового файла. Так если (fo=2;), то будет создан новый файл с именем (2.jpg). Расширение указывать не надо. Новый файл будет копией файла 1.jpg. То есть один файл картинки мы уже создали. Пока это просто копия. Ну и если (sa=-2), то картинка просто будет спасена в файл без показа. Это важно при работе в пакетном режиме, когда сразу обрабатывается очень много файлов.
Чтобы было понятно дальше я хочу объяснить, что картинки в файлы формата (jpg) записываются в закодированном виде. Это делается для того, чтобы файл был меньше размерами. Тогда его легче передавать через интернет и записывать на флешки. И очень важная работа состоит в том, чтобы числа из файла превратить в полную числовую матрицу картинки. Вот такой вид и хранится в памяти. А если надо записать в файл, то снова делается кодирование для уменьшения размера файла. И данная команда все это проделывает автоматически и молча. Пользователю не нужно об этом думать.
Перейдем теперь на более высокий уровень. Пусть будет (mo=1). В этом случае программа делает более сложную работу и использует информацию из еще 6 параметров. Их имена (tw), (th), (wid), (hei), (xs), (ys). А номера в массиве s() от 12 до 17 подряд. Смысл у них такой: tw, th (total width, height) -- полные ширина и высота, wid, hei (width, height) -- ширина и высота фрагмента, xs, ys (xshift, yshift) -- сдвиг фрагмента из левого нижнего угла. Если все эти параметры будут отрицательными, то команда сделает то же, что и при (mo=0). А если они положительны или 0, то будет иначе. Прежде всего, картинка будет промасштабирована к размерам tw, th. При этом необходимо указать еще один параметр sc (scale). Он имеет значения от 1 до 5 и указывает тип интерполяции при масштабировании. Какой режим больше вам понравится лучше проверить эмпирически. Если один из двух указанных параметров равен -1, то он будет определен с учетом аспектного отношения оригинала.
Дополнительно уже промасштабированная картинка будет использована, чтобы из нее вырезать фрагмент с размерами (wid) и (hei) и с учетом сдвига на (xs) и (ys). И уже только фрагмент будет показан или спасен в файл. Это будет уже новая картинка, созданная программой на языке ACL. У нас уже достаточно информации, чтобы написать программу, которая покажет картинку, из которой пользователь вырежет фрагмент мышкой и программа покажет этот фрагмент и запишет его в файл. Я сразу покажу код этой программы
#d 6 s(12) 800 -1*5 #w [op=im; mo=1; sc=1; sa=-1; file=1.jpg; form=2;]
# xs=s(102); ys=s(103); w=s(104)-xs; h=s(105)-ys;
#d 6 s(12) -1*2 w h xs ys #w [op=im; mo=1; sc=1; sa=-1; file=2.jpg; form=3;]
Здесь в первой строке определяем значения 6-ти указанных параметров. Конструкция -1*5 указывает, что значение -1 надо повторить 5 раз. Эта команда берет картинку из файла (1.jpg), увеличивает ее горизонтальный размер до 800 пикселей, показывает на экране и спасает в файл (2.jpg). Пользователь должен поставить курсор мыши в левый нижний угол фрагмента, затем нажать левую клавишу и не отпуская ее передвинуть курсор в правый верхний угол, а потом отпустить клавишу. Картинка закроется, программа получит нужные координаты и снова вызовет эту же команду, но с файлом, который только что был создан. И уже без масштабирования просто вырежет указанный фрагмент. Снова спасет картинку в файл (3.jpg) и покажет ее на экране.
Имея ПИ все это легко проделать. Интересно, что команда третьей строки указывает имя исходного файла в заголовке окна, который читался, хотя показывает фрагмент. Дело в том, что новый файл еще не создан. Это можно исправить, но и так все работает. Файл (3.jpg) создается, и там именно то, что было показано. У читателя уже достаточно сведений, чтобы написать более сложную программу, которая покажет первую картинку с именем (1.jpg), из которой можно вырезать фрагмент, а затем она вырежет такой же фрагмент из файлов с именами (2.jpg), (3.jpg), и так далее хоть до 1000. Однако я сам предпочитаю записывать файлы с именами одинаковой длины, например, от 001 до 999. Так они лучше упорядочиваются в каталоге файлов. На всякий случай я покажу и такой код.
#w [op=im; mo=0; sa=0; file=1/001.jpg;]
# xs=s(102); ys=s(103); w=s(104)-xs; h=s(105)-ys; j=1; n=20; #d 6 s(12) -1*2 w h xs ys
#rep n #w [op=im; mo=1; sc=1; sa=-2; file=\u49;/\I-3 j;.jpg\E fo=\u50;/\I-3 j;\E] # j=j+1; #end
Здесь сначала показывается первая картинка из папки с номером 1 внутри рабочей папки, где находится вызываемая ACL программа, она определяется автоматически, если запускать программу из редактора. Нужно вырезать фрагмент. Координаты преобразуются в параметры команды с вырезанием фрагмента и затем открывается цикл повторить все 20 раз. Команда вырезает фрагмент и сразу записывает в файл, ничего не показывая. Затем счетчик (номер файла) увеличивается на единицу и все повторяется с новым файлом. Важным моментом команды, которая вырезает фрагмент в цикле, является то, что имена файлов, которые читаются и куда записываются надо обязательно писать, начиная с команды форматирования, то есть с символа (\). Только в том случае, когда первым символом стоит команда форматированного текста ПИ воспринимает аргумент как такой текст. При любом другом символе текст воспринимается как простой и закрывается символом (;), то есть точки с запятой.
Так получилось исторически. Сначала аргументы были просто текстом. Потом оказалось, что нужны форматированные тексты. Но и старый режим хотелось оставить. В простых случаях он более удобный и легче понимается. По этой причине числа 1 и 2 здесь записаны своими юникодами как (\u49;) и (\u50;). Только в этом случае строка начинается с команды. Но я уже показывал раньше вариант, когда имя файла можно предварительно напечатать командой pr, а затем указать в параметре (\Tp). Тогда использовать юникоды не придется. Правда два текста таким способом определить не получится. В указанном коде так устроено, что пронумерованные файлы читаются из папки с номером 1, а результат, записывается в папку с номером 2 с теми же именами файлов. Это удобно, но минус в том, что файлы должны быть пронумерованы. А нельзя ли просто обработать все файлы из папки 1 с произвольными именами.
Разумеется можно и это. И делается это опять же не так уж и сложно. Каталог файлов в папке читает команда работы с файлами. Она так и называется file, но можно писать одну букву f. Код новой и уже достаточно продвинутой программы показан ниже
#f [op=fold; file=intro;] # u=KY-9999; s(3)=u; #f [op=fcat; file=\H 1\E] # a=u; b=s(5); # &=b<1;
#case 0 #pr Folder [\H 1] inside ACL program folder is empty !\nPlease improve problem !\E #m [op=win;] \Tp\E #end |
#case 1 #te [op=find; b=a; le=b; n=1; c=124;] # n=s(1); i=a; j=1; d=i(j)-i; #w [op=im; mo=0; sa=0; file=arg;] 1/\Ti d\E
. # xs=s(102); ys=s(103); w=s(104)-xs; h=s(105)-ys; #d 6 s(12) -1*2 w h xs ys
. #rep n # d=i(j)-i; g=d-4; #w [op=im; mo=1; sc=1; sa=-2; file=arg; fo=arg;] 1/\Ti d\E 2/\Ti g\E # i=i(j)+1; j=j+1; #end
#end |
Здесь появилось много новых элементов кода, о которых я сейчас расскажу. Команда f тоже имеет много операций. Операция [fold] устанавливает рабочую папку внутри папки ПИ. Я уже писал об этом выше. Это бывает удобно в том плане, что после ее установки адреса всех файлов отсчитываются от нее. И их можно записать более коротким способом. Текстовый массив имеет 1999999 символов в виде двухбайтовых юникодов. Но максимальный номер, который можно использовать в современной версии программы определяет переменная KY. Чтобы не портить весь остальной код, каталог разумно записать в конец массива, выделяя для него какое-то место, например 9999 символов. Переменная (u) как раз и определяет начало записи каталога и параметр s(3) устанавливается на это начало. И вот операция [fcat] команды f прочитывает каталог файлов из папки с именем, который устанавливает параметр [file]. Для этой операции рабочая папка не используется и надо писать полный адрес относительно папки ПИ. Но команда (\H) как раз и записывает адрес рабочей папки, который был определен ранее. Можно было бы поставить его явно, но удобнее так, потому что папку можно изменить, а запись адреса в таком виде менять не придется. Замечу, что после всех команд форматирования текста пробелы игнорируются. Их удобно писать для того, чтобы код был более понятным.
Каталог записывается так же, как и команда pr, то есть после записи параметры s(4) и s(5) содержат начало и длину записи. Удобно их запомнить в переменных (a) и (b). Далее проверяем переменную (b) на ноль. Если ноль, то пишем, что такой папки не существует. Тут надо объяснить как это работает. Переменную (&) мы уже видели. Здесь она вычисляется. Но к обычным операциям сложения, вычитания, деления, умножения в языке ACL добавлены операции поиска минимума и максимума. При этом конструкция (b<1) дает в результате (b) если (b) меньше 1 и 1, если больше или равна. А команда case -- это тоже цикл, но с условием. Она имеет один аргумент. И работает так, что если аргумент равен значению переменной (&), то последующий код выполняется, а если не равен, то не выполняется. И так же, как в команде цикла, учитывается весь код до команды end. Но тут есть особенность. Дело в том, что в данном случае эта команда снова проверяет то же самое условие. И если оно выполняется, то весь код повторяется снова. А если нет, то не повторяется.
То есть если переменную (&) не переопределить, то код будет выполняться бесконечно долго и программа зависнет. Такая неприятность реально существует. Иногда удается цикл остановить, а иногда таки не удается. И приходится снимать программу средствами операционной системы. Но это бывает редко и надо стараться следить за этим. Для сокращения записи переопределения переменной (&) у команды end тоже может быть аргумент в виде символа вертикальной черты через пробел. Такая запись принудительно изменяет (&) на значение 12345, и цикл выполняется только один раз. То есть команда case может быть использована и как оператор цикла по условию, и как просто условный оператор. Итак, если (b=0), то папка задана неправильно, ее не существует, и работа не будет сделана, а пользователь получит сообщение об этом. А если (b > 0), то работаем дальше.
Команда te (text) работает с символьным массивом. У нее есть операция [find]. Она ищет все позиции символа с юникодом, который определяет параметр (c), более полное имя code. Просматривается кусок массива, начиная от номера (b) и длиной (le). Эта пара параметров всегда указывает куски массивов. Фактически это аналоги имени и размера массивов в других языках. А параметр (n) указывает начало целого массива i(), куда будут записаны найденные номера. Дело в том, что каталог выдается в виде одной строки, где имена файлов разделены как раз символом вертикальной черты. Точнее этот символ заканчивает каждое имя файла. В конце выполнения этой операции параметр s(1) будет равен числу найденных символов, то есть числу файлов в каталоге. Это число запоминаем в переменной (n). Затем ставим счетчик (j) на 1 и определяем начало и длину первого имени файла в каталоге. Начало находится в переменной (a), а длина равна (d=i(1)-a).
Наконец можно смотреть первую картинку. Дальше стоит уже знакомая нам команда. Но она снова странно написана. Тут история такая. Дело в том, что символьные параметры (file) и (form) имеют фиксированную максимальную длину 42 символа. И раньше этого хватало с запасом. Но последнее время есть любители писать длинные имена файлов и папок. Я сам так никогда не делаю, но кто-то возможно сделает. И тогда надо переходить на более общую форму. В параметре (file) пишется значение arg (argument), и это указание на то, что имя файла надо читать из аргумента команды. Там оно и записано. Файл имеет имя (\Ti d) и находится в папке 1 относительно рабочей папки.
Следующая строка полностью повторяет уже известный нам код. А в цикле мы снова определяем две длины имен файлов, причем вторая на 4 символа меньше. А команда записи фрагмента файла снова имеет параметры (file) и (form) в виде аргументов. Теперь первый указывает на тот же самый файл. А второй меняет папку с 1 на 2 и записывает имя файла без расширения, потому что расширение всегда (jpg) и его писать не надо. Затем надо поменять начало имени файла и номер элемента массива, где записан следующий символ вертикальной черты. И такой код прекрасно выполняет всю работу. Замечу, что работать с файлами в пакетном режиме очень удобно. И таких работ бывает много. Данный код можно использовать как эталон для большого числа операций с файлами.
И уж совсем необычно. Дело в том, что чтение параметра (file) из аргумента я сделал давно. А вот то же самое для параметра (form) я сделал, когда писал эту статью первый раз. Раньше этого не было. Это работает только в версиях ПИ после 10 апреля 2022 года. ПИ уже редко изменяется, так как почти все сделано. Но иногда бывают доработки и добавление возможностей. А в старых версиях можно записать параметр fold в явном виде.
Иногда, в более сложных программах, в качестве входной картинки нужно использовать не картинку из файла, а картинку, которая уже была спасена в тот самый шкаф с ящиками, о котором я писал выше. Для этих целей команда используется с параметром (mo), значения которого равны 2 и 3. При (mo=2) картинку можно только масштабировать, используя параметры (tw) и (th). А при (mo=3) из картинки можно вырезать фрагмент, используя параметры (wid), (hei), (xs), (ys). Номер картинки из шкафа задается параметром (n), то есть (number) в интервале от 1 до 100. Разумеется, что сначала картинку надо в шкаф положить.
Команда w всегда записывает картинки в формате (jpg). Но если нужно записать картинку в формате (png), то это тоже возможно. Это делает снова команда f. Ведь речь идет о записи файла. Эта команда выглядит так
#f [op=topng; fo=; n=;]
Тут все просто. Параметр [fo] снова указывает имя файла без расширения, [n] указывает номер спасенной картинки. А спасает картинку команда w. Но не только она. В языке есть две команды g и eg, которые позволяют рисовать картинки с нуля. Они тоже спасают картинки либо в (jpg) файл, либо в шкаф. Надо сказать, что шкаф с картинками очень удобен для передачи из одной команды в другую. Это работает намного быстрее, чем через файлы.
В этом месте удобно обратить внимание читателя на то, что операций конвертирования файлов картинок немного больше, чем та, что указана выше. И некоторые команды сделаны сразу в более широком виде. Я просто укажу некоторые из них. Команда
#f [op=tobm; file=; fo=; dir=; n=; col=;]
конвертирует картинку из файлов типа (jpg), (png), (gif) в byte-map файл. В этом файле каждый байт описывает уровень серого от 0 до 255. При этом, как обычно параметр [file] должен указывать имя графического файла, например, [file=one.jpg;]. Однако, если [file=here;], то картинка будет считана не из файла, а из шкафа и ее номер будет [n]. Такая картинка должна быть предварительно записана. В результате операции будет создан новый файл с именем, заданным параметром [fo] как графический файл в новом формате. Имя надо писать вместе с расширением, оно может быть любым. Этот формат нестандартный, некоторые его называют (raw), то есть необработанный.
Параметр [dir] (direction) определяет направление записи по вертикали. Если [dir=1;], то запись идет в направлении сверху вниз, обычном для графических файлов. Для любого другого значения, например [dir=0;], картинка записывается начиная с нижней строки вверх, как это делается во всех расчетных изображениях, записанных на языке ACL. Как обычно, элементы строк картинки записываются подряд. Ширина картинки возвращается в параметр s(12), а высота -- в параметр s(13). Цветные картинки преобразуются в серые по закону скалярного произведения с заданным цветом, номер которого в массиве цветов задает параметр [col]. Пусть этот цвет имеет компоненты R,G,B. Тогда цвет каждого пиксела приводит к уровню серого g по закону g=(r*R+g*G+b*B)/255), но внутри интервала (0,255). Такой способ позволяет применять цветные фильтры при конвертировании картинки, а также менять ее яркость. Размер записанного файла в байтах равен числу пикселей в картинке.
Параметр [col] нам уже встречается не первый раз. Пора объяснить как это устроено. Как я уже писал, цвета описываются тремя байтами, то есть числами от 0 до 255 для красного, зеленого и синего. Но писать каждый раз три числа скучно. Поэтому ПИ использует массив цветов из 256 элементов, в котором для каждого элемента записаны 3 значения. Число элементов не такое уж и большое и все цвета (миллионы) не записать. Но это и не требуется. Массив в любой момент можно переопределить. Для этого есть команда col, о которой уже была речь выше. Она позволяет задать произвольные номера цветов и после этого их можно использовать. ПИ в самом начале все цвета определяет. Но такого определения не всегда хватает. И все же я перечислю как цвета определяются в самом начале работы программы: (1 -- 243) черный (0 0 0), (244) темно-красный (128,0,0), (245) темно-серый (85,85,85), (246) белый (255 255 255), (247) черный (0 0 0), (248) красный (255 0 0), (249) синий (0 0 255), (250) зеленый (0 195 0), (251) серый (128 128 128), (252) коричневый (152 128 0), (253) фиолетовый (152 0 152), (254) голубой (0 255 255), (255) темно-синий blue (0 0 128), (256) светло-коричневый (220 200 180).
Следующая команда аналогична предыдущей, но работает только с цветными картинками и записывает цвета точно. Она имеет вид
#f [op=tocm; file=; fo=; dir=; n=;]
Здесь все точно так же, только результатом является color-map файл, в котором каждые три байта описывают уровень красного, зеленого и синего от 0 до 255 для одной точки рисунка (пиксела). Параметр [col] не используется, а размер файла в байтах в три раза больше, чем число пикселей в картинке. И есть еще более экзотический конвертор, команда
#f [op=tops; mo=; uni=; file=; fo=; n=;]
Здесь с входным файлом все точно также, а в результате операции будет создан новый файл с именем, заданным параметром [fo] как графический файл в формате (eps). Имя файла надо указывать вместе с расширением. Оно не обязано иметь расширение (eps). При этом параметр [mo] должен быть 0, 1, 2, 3, 4 или 5. Значение 0 приводит к созданию черно-белого eps-файла, значение 2 - к фрагменту этого файла, который описывает картинку. Этот фрагмент можно использовать в команде ps для создания комбинированной картинки. Значение 1 приводит к созданию цветного eps-файла, значение 3 - к фрагменту этого файла. Значения 4 или 5 описаны ниже. Другие значения приводят к ошибке. Параметр [uni] определяет дополнительно масштабирующий фактор для картинки в режимах [mo=0,1;], чтобы получить соответствие размеров eps-картинки на экране исходной картинке. Этот фактор равен отношению пиксела экрана к PS точке в единицах 0.0001. Например, пусть компьютер имеет 1024 пиксела на размере экрана 28.42 см. Когда используется программа GSview в режиме увеличения, показывающем бумагу формата A4 (595 точек) на размере экрана 26.4 см, отношение будет 0.6255. С этим значением программа GhostView показывает картинку точно также, как и ACL интерпретатор. Однако, это соотношение может быть другим на других компьютерах. Каждый пользователь может определить отношение эмпирическим путем. Иногда очень важно иметь соответствие каждого пиксела каждой точке экрана так как интерполяция приводит к артефактам.
Указанные операции обычно отсутствуют в других языках программирования или сделаны в виде готовых программ. На самом деле они очень помогают манипулировать с картинками без каких-либо ограничений. Как это делать будет написано позднее. Язык postscript (PS) для описания графики является очень мощным и универсальным. Иногда его полезно использовать и мой язык ACL как бы дает удобные средства для работы на языке PS.
5. ДЕЛАЕМ НОВУЮ КАРТИНКУ ИЗ ЧИСЛОВОЙ МАТРИЦЫ.
Важным элементом научной графики, да и не только научной, является изображение числовой матрицы. Числовую матрицу можно вытащить из самой картинки. Например, для форматов (jpg), (png), (gif) для этого можно использовать указанные выше операции #f [op=tobm;] или #f [op=tocm;]. Из других форматов матрицу можно вытащить другими способами. А часто числовую матрицу можно просто вычислить. Для этого и существует язык программирования ACL. Иногда числовую матрицу вычислить совсем просто, если нужно показать простые зависимости типа синуса или гаусса. Иногда расчет требует решения сложных уравнений и занимает много времени. Но всегда такие картинки нужны. Указанную работу выполняет все та же операция #w [op=im;] но при других значениях параметра [mo].
Числовые матрицы могут иметь очень много значений, и их удобно записывать в коде компьютера. По крайней мере мне так удобно. Если матрица записана текстом, то прочитать текст и конвертировать в код компьютера совсем не сложно. Сложность как раз в том, что и в коде компьютера числа можно записывать разными способами и все эти способы используются. Я перечислю какие способы есть. Все эти способы в операции различаются значением параметра (mo). Итак, если [mo=8;] то данные внутри файла с матрицей есть целые числа размером 8 бит (один байт). Если [mo=16;] то данные внутри файла с матрицей есть целые числа размером 16 бит (два байта). Если [mo=24;] то данные внутри файла с матрицей есть цвета пикселей (красный, зеленый и синий) в 3-х байтах для каждой точки. Если [mo=32;] то данные внутри файла с матрицей есть реальные числа размером 32 бита (четыре байта). Если [mo=100;] то данные внутри файла с матрицей вычисляются (см. далее). Если [mo=125;] то данные внутри файла с матрицей записаны в файл по 8 пикселей в один байт (черно-белое изображение).
Легко понять, что данные при mo=8 дает операция #f [op=tobm;], а данные при mo=24 дает операция #f [op=toсm;]. Данные при mo=32 обычно вычисляет сама программа и потом записывает в файл в формате float. Данные при mo=125 иногда дает сканер при сканировании черно-белых книг. Это самый сжатый формат, когда каждый пиксель может быть либо черным. либо белым. Для книжного текста без картинок этого достаточно. Данные при mo=16 часто дают детекторы электромагнитного излучения, которые считают фотоны. Числовые матрицы часто записывают в формат tiff, где они также сопровождаются информацией о размере картинки, способе записи, дате измерения и о многом другом. Вытащить матрицу из файла нетрудно. Но бывают и другие форматы и можно самому так записать. Самая общая структура такой команды для показа числовых матриц записывается так
#w [op=im; mo=; file=; fo=; le=; ord=; sty=; bot=; top=; b=; nx=; ny=; tw=; th=; wid=; hei=; xs=; ys=; sa=; em=; xp=; yp=; pa=;]
Про параметры mo, file, fo мы уже все знаем, они такие же как и раньше. Данные берутся из файла и параметр [le] показывает размер заголовка файла в байтах. Обычно заголовок -- это некоторый текст, который предшествует данным в файле. Его надо пропустить перед чтением матрицы чисел, чтобы получить правильные значения. Однако если [mo=32;] то возможен специальный случай [file=here;] который означает, что данные будут взяты из вещественного массива r(), начиная с первого элемента с индексом [le] вместо того, чтобы читаться из файла. Этот случай полезен, когда данные непосредственно вычислены или приготовлены из нескольких источников.
Если [mo=16;], то параметр [ord] определяет порядок байтов при записи целого числа. Так если [ord=0;], то LowByteSecond (младший байт второй). В противном случае если, например, [ord=1;], то LowByteFirst (младший байт первый). Реально в файлах могут быть реализованы оба случая. LowByteFirst использует ОС Windows, а LowByteSecond -- Unix и Java.
Параметры [sty], [bot=1;], [top=99999;] задают стиль показа данных для [mo] = 16, 32 и 100. В этом случае диапазон значений превышает возможности графики и необходимо преобразование. Численные данные имеют минимальное значение (Fmin) и максимальное значение (Fmax). Эти значения для [mo=100;] всегда задаются в элементах вещественного массива r(j) и r(j+1), где индекс j определяется параметром [b=j;]. Для [mo=16;] или [mo=32;], они задаются, если abs([sty]) > 10, и определяются автоматически в противном случае. При автоматическом определении эти значения возвращаются в те же элементы реального массива. Значение каждой точки данных показывается в пределах от 0 до 255 (8 бит). Этот диапазон получается масштабированием из области значений данных с началом Fmi и концом Fma, которые определяются по формуле
Fmi = Fmin + Dff*[bot]/100000, Fma = Fmin + Dff*[top]/100000, Dff = Fmax -- Fmin.
Тип масштабирования задается остатком от деления [sty] на 10. Пусть это будет rsty. Масштабирование линейное если rsty=1 и делается по формуле pix = 255*(f - Fmi)/(Fma - Fmi). Оно логарифмическое если rsty=2 и делается по формуле pix = 255*log(f/Fmi)/log(Fma/Fmi). Если rsty=3, то оно вычисляется по квадратному корню, а именно pix = 255*sqr((f - Fmi)/(Fma - Fmi)). При этом отрицательные значения заменяются нулями. Обычно минимум черный, максимум белый. Однако если параметр [sty] отрицательный, то контраст противоположный. Целые параметры [bot] и [top] задают часть области внутри интервала (0,1) в единицах 0.00001. Поэтому они должны иметь значения от 1 до 99999. Наконец, каждый пиксель данных может быть показан прямоугольником имеющим [nx] и [ny] пикселей экрана горизонтально и вертикально.
Параметры tw, th, wid, hei, sa уже рассматривались нами ранее. Остается описать параметры em, xs, ys. Тут все просто. Первоначально компьютеры были слабые и на экране было мало точек. И я все картинки рисовал в центре экрана. Но время шло и все менялось. Приходилось менять и язык ACL. И хотелось, чтобы и старые программы работали без изменений и новые. И я придумал такой трюк, что ввел специальный параметр em, который при нулевом значении не учитывал новое и ПИ работала как раньше. А если он больше нуля, например, 1 или 2, то ПИ работала по новому. При первом запуске em всегда 0 и нет проблем. А если я хочу по новому, то его надо изменить на значение больше нуля. И вот если [em=0;] то параметры xs и ys игнорируются, а окно с картинкой рисуется в центре. А если [em=1;] то они показывают сдвиг левого верхнего угла окна из левого верхнего угла экрана. Такой режим мне последнее время нравится больше, так как я стал ставить туда окно ПИ, а раньше оно было на весь экран.
Самый последний параметр (pa) тоже появился позднее других. Дело в том, что первоначально, я числовые матрицы рисовал как серые карты так, что минимум черный, максимум белый или наоборот. Но время шло и ситуация менялась. Начали рисовать цветные карты. Пришлось и мне это сделать. Делается это так. Весь интервал значений от 0 до 255 ставится в соответствие некоторым цветам. Для такого соответствия нужна палитра цветов, то есть 256 цветов. Это соответствие можно задавать разными способами. Первоначально я цвета вычислял. Это работает при (pa = 0, 1 и 2). При этом 0 соответсвует старому черно-белому (серому) режиму, 1 и 2 двум цветным режимам. Но потом я решил, что лучше такую таблицу цветов записывать в файл и пусть программа все читает из файла. Сейчас такой файл с названием (colmap.txt) является составной частью ПИ. Он используется при [pa=3;]. Удобство такого подхода в том что для замены карты цветов достаточно просто поменять файл и все.
Все указанные параметры являются элементами служебного массива s() в следующем порядке: . . . b (9), le (10), mo (11), tw (12), th (13), wid (14), hei (15), xs (16), ys (17), sty (18), bot (19), top (20), . . . . . nx (21), ny (22), sa (23). . . . Поэтому при определенном навыке можно определить значения всех параметров командой #d 16 s(9) 1 2 3 . . . Рассмотрим конкретный пример. Ниже показан код программы
# nx=300; ny=300; J=101; j=J; y=0; d=0.02; #rep ny # y2=y*y; x=0;
#rep nx # a=sin(x*x+y2); r(j)=a*a; j=j+1; x=x+d; #end # y=y+d; #end
#p [tw=nx; th=ny; wid=nx; hei=ny; xs=0; ys=0; em=1; xp=10; yp=40; pa=3;]
#w [op=im; mo=32; file=here; fo=2; le=J; sty=1; bot=1; top=99999; nx=1; ny=1; sa=-1;]
А результат выполнения этой программы показан на рисунке справа. Здесь использована команда p (parameters). На самом деле эта команда ничего не делает и используется только для задания параметров в квадратных скобках. Это бывает удобно когда часть параметров в цикле не меняется, а другая часть меняется. В данном случае сначала выделены как бы общие и универсальные параметры, а в самой команде w остались только реально существенные параметры. Зависимость, показанная на рисунке -- это квадрат синуса от квадрата радиуса с центром в левом нижнем углу. В отличие от многих других программ ACL показывает зависимость от вертикальной координаты снизу вверх, а не сверху вниз, как рисуются все картинки на компьютере. Такой порядок соответствует правильному направлению осей координат.
Режим с mo=32 и file=here является основным при показе расчетных зависимостей. Остальные режимы полезны при показе числовых матриц, записанных без сжатия в некоторых типах файлов. Так, например, ПИ не может показать сразу tiff файл с 16-битной матрицей как картинку. Но она может показать его как числовой файл и одновременно конвертировать в (jpg) или (png) формат. Использование числовых матриц -- это очень мощный инструмент для преобразования картинок. К числовым матрицам можно применять любые математические преобразования вплоть до самых экзотических.
Самый простой пример -- это умножение картинок. Причем одну картинку можно взять из файла, а другую нарисовать и потом умножить. Ниже я покажу пример как это работает. Прошлый пример нарисовал картинку и записал ее в файл (2.jpg). Она имеет размер 300*300 пикселей. Мы можем вытащить из файла числовую матрицу этой картинки командой, о которой я уже писал выше. Затем нарисовать другую картинку и перемножить два массива чисел, а потом снова нарисовать картинку и записать в файл. Код такой программы показан ниже
# nx=300; ny=300; n=3*nx*ny; J=101; J1=J+n; #f [op=tocm; file=2.jpg; fo=3.cm; dir=0;]
#io [op=rb; fir=r(J); file=3.cm; n=n; le=0;] # j=J1; y=-ny/2; R=120;
#rep ny # y2=y*y; x=-nx/2; #rep nx # a=1-int(sqr(x*x+y2)/R); #d 3 r(j) a*3 # j=j+3; x=x+1;
#end # y=y+1; #end #ma [op=vvm; b=J; le=n; trx=J1-J;] #io [op=wb; fir=r(J); file=4.cm; n=n;]
#w [op=im; mo=24; file=4.cm; fo=5; le=0; sa=-1; wid=nx; hei=ny; xs=0; ys=0; em=1; xp=10; yp=40;]
Здесь сначала в переменные засылаются значения числа пикселей по обоим направлениям, затем общее число чисел в файле. Первая команда первой строки вынимает из файла картинки числовую матрицу и записывает ее в файл. Она так сделана, что в числовой массив она не записывает. Поэтому вторая команда как раз берет данные из этого нового файла и записывает их в числовой массив. Данные берутся побайтно, а записываются в реальный массив, у которого каждый элемент имеет 8 байтов. Это не расточительно? Увы, но для упрощения языка и работы в нем есть только реальный массив, который имеет большой размер и вся работа идет с ним. Обработка картинок все равно делается мгновенно и тут экономить нет смысла. Описания всех команд есть в интернете и можно получить полную информацию что каждая из них делает. Удобно искать описания из таблицы по адресу .
Затем в другой массив мы записываем 1 внутри круга определенного радиуса и 0 вне этого круга. После этого два массива чисел перемножаются и результат записывается в новый файл снова побайтно. А потом этот новый файл рисуется в виде картинки, которая показывается и записывается в файл. Результат работы этой программы показан на рисунке справа. Вообще говоря, чтобы экономить память и упростить работу я сделал также команду bi, которая работает непосредственно с матрицами цветных картинок. Для манипуляций с одной или двумя картинками формата (jpg) можно использовать эту команду. При этом совсем не надо считывать матрицу побайтно из файла в числовой массив.
Но если использовать расчетные картинки, то это необходимо. Правда есть и другой сценарий. Можно расчетную картинку записать в файл формата (jpg) и потом работать так, как описано выше. При считывании и записи байтов из файла надо помнить, что байты -- это целые числа в диапазоне от -128 до 127. А коды символов и цвета картинок -- это целые числа в диапазоне от 0 до 255. И в языке ACL даже есть специальная операция преобразования байтов в цвета. Это #ma [op=vba;]. Фокус в том, что компьютер записывает отрицательные числа как числа в диапазоне от 128 до 255 автоматически, но в обратном порядке. То есть -1 == 255, а -128 == 128. Просто к отрицательным числам прибавляется число 256. Это период. Именно поэтому в нашем примере умножение на 0 и на 1 не испортила чисел даже при том, что они неправильно были записаны. А вообще-то необходимо байты преобразовывать в коды цветов и только потом производить математические преобразования.
Показанный код фактически делает клип, то есть вырезает из картинки кусок. Из другой картинки можно сделать обратный клип, то есть поменять 0 и 1 местами, и оставить только ту часть, которая исчезла тут. Затем обе картинки можно сложить, используя команду bi. Как команда bi складывает картинки я покажу на следующем примере. Вот код программы
#f [op=tocm; file=06.jpg; fo=06.cm; dir=0;] #f [file=08.jpg; fo=08.cm;]
#d 2 i(1) 1 1 #bi [op=sup; mo=0; file=list; fo=09.cm; b=1;] 06.cm|08.cm\E
#w [op=im; mo=24; file=09.cm; fo=08; le=0; sa=-1; wid=300; hei=300; xs=0; ys=0; em=1; xp=10; yp=40;]
А результат показан на картинке справа. Я объясню что тут показано. Из последней показанной картинки (ее номер 7) я вырезал фрагмент из середины с полной шириной и половинной высотой и записал ее с именем 08. Это сделано с помощью внешней программы. Затем я из картинки 6 (предпоследней) и новой картинки вынимаю числовые матрицы bi (byte image). И применяю команду сложения. Сначала в целом массиве надо задать веса каждой картинки. Я взял одинаковые, имеет значение только соотношение, сами значения роли не играют. Затем я указал операцию sup, модификацию mo, указал что файлы будут списком в аргументе, указал имя новой матрицы и индекс массива i(), где записаны веса. А в аргументе имена файлов. Ну и последняя команда такая же, как у предыдущей программы. Только матрица имеет номер 9, а картинка 8.
Как видно на рисунке, размер матрицы равен той, которая была в первом файле. Вторая матрица может иметь меньший размер, она все равно целиком прочитывается и складывается. Но чтобы результат был разумный необходимо, чтобы ширина второй картинки совпадала с первой. Так как матрицы чисел не знают про ширину картинки, то они складываются как одномерные массивы. После этого весь интервал значений приводится к (0, 255) масштабированием. Видно, что максимальная яркость осталась только там, где картинки складываются. Там где нет второй картинки яркость стала в половину меньше. Складывать можно произвольное число произвольных картинок с произвольными весами. Веса также могут быть отрицательными, тогда картинка вычитается.
С помощью команды bi картинки можно не только складывать, но и умножать и даже делить. Есть и набор преобразований одной картинки. Команда #bi все делает чуть проще, чем через реальный массив, но и через него тоже можно работать. Я просто скажу без детального описания, что то же самое (через реальный массив) можно делать и с 16-битными числовыми матрицами в файлах типа tiff и им подобных. Среди готовых программ, уже написанных мной, есть команда (Img pro), в которой реализованы некоторые из возможных операций с картинками.
6. НАУЧНАЯ ГРАФИКА.
Научная графика -- это способ представления численных результатов в виде картинок. Есть много готовых программ, которые это делают. Эти программы различаются способом ввода численных результатов, параметров картинок и методами рисования самих этих картинок. В языке ACL все это сделано мной и давно, причем в таком виде, какой нравится лично мне. Разумеется, вид можно поменять и можно сделать так, как в других программах, то есть с интерфейсом. Более того, все это уже сделано. Но тут я покажу как быстро и легко можно делать рисунки в рабочем варианте. То есть в процессе работы. Что касается рисунков для научных публикаций, то я их делаю на языке postscript, который не привязан к экрану монитора, делает векторную графику и легко преобразовывается в формат (pdf).
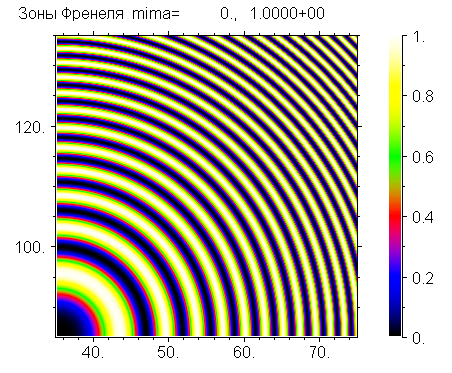О том, как показывать матрицы чисел картинкой я уже написал, но для отчета на картинке также должны быть оси координат, какие-то тексты, и шкала соответствия цветов и значений функции. Такого типа картинки показывают разные варианты суперкоманд. Я покажу как используются наиболее продвинутые из них. Сначала посмотрим код программы и результат, а потом комментарии.
# nx=300; ny=300; n=nx*ny; J=101; j=J; y=0; d=0.02; #rep ny # y2=y*y; x=0;
#rep nx # a=sin(x*x+y2); r(j)=a*a; j=j+1; x=x+d; #end # y=y+d; #end
#d 2 r(1) 85 135 #e [n=5;] _scom #pas 5 r(1) r(6) #d 2 r(1) 35 75 #e [n=5;] _scom
#d 6 A J nx ny 1100 11 1 #p [pa=3;] #pr 09|Зоны Френеля\E #e [n=2;] _scom
Легко заметить, что здесь первые две строчки уже были написаны в одной из предыдущих программ. Они вычисляют все тот числовой массив, что и на рисунках в конце предыдущего раздела. И делают ту же картинку. Но теперь эта картинка находится в квадрате числовых осей (в общем случае, в прямоугольнике), которые размечены правильным образом. Над картинкой есть подпись и есть шкала соответствия цветов и значений функции. Автоматическая разметка оси не такое уж и простое дело. Поэтому я сделал суперкоманду с номером 5, которая это делает. В третьей строке в первые два элемента целого массива вводится два числа и затем эта суперкоманда добавляет к ним еще 3 числа. После этого 5 чисел нужно сдвинуть дальше и повторить то же самое для оси Х. Теперь все готово для использования суперкоманды с номером 2, которая и делает рисунок.
Для нее в переменных (A), (B), ... надо задать 6 значений, а именно, начало числового массива, число точек по обеим осям, указатель на показ картинки и масштабирование, число пикселей по обеим осям и начало массива, где записана разметка осей. После этого надо указать палитру и напечатать два текста. Первый -- это имя файла без расширения, второй -- заголовок. Расширение всегда png. На показ графика указывает единица в 4-м разряде переменной (D). Если ее не будет, то график записывается в файл но не показывается. Так суперкоманда работает в цикле. Есть еще и 5-й разряд. Если он равен единице, то контраст обращенный. А первые три разряда указывают на масштабирование в процентах. Имеет значение также знак (D). Если он минус, то показывается голая картинка. При этом запись суперкоманды короче, чем было описано выше, хотя компьютер работает дольше.
В переменной (E) каждый разряд указывает число пикселей экрана на 1 точку матрицы. В стандартном режиме функция нормируется на интервал (0, 1), а реальные минимум и максимум показываются над графиком. Так сделано потому что эти значения могут быть весьма большими и показывать их на оси не очень удобно. Но если переменная (E) имеет знак минус, то показываются реальные значения на оси функции и необходимо указывать разметку этой оси после разметки осей X и Y. Размер текста автоматически определяется размером картинки. Есть и другие суперкоманды для рисования числовых матриц, но эта самая продвинутая и я сам чаще всего ее использую.
Наиболее часто приходится рисовать одномерные графики, то есть зависимость только от одного аргумента. Такие суперкоманды тоже существуют, причем разные, когда какая лучше подходит. Я покажу тоже только одну, которая является универсальной и наиболее продвинутой. Она рисует сколько угодно кривых разными цветами, но цвета нужно определять. Есть предопределенные цвета и об этом я уже написал выше, но их немного. Я снова покажу пример использования такой суперкоманды и результат ее работы. Результат, как всегда справа, а код примера ниже.
# nx=300; ny=15; n=nx*ny; J=101; j=J; y=0; d=0.02;
#rep ny # y2=y*y; x=0; #rep nx # a=sin(x*x+y2); r(j)=a*a; j=j+1; x=x+d; #end # y=y+d*5; #end
#d 7 A J nx 15 -1 1 247 1100 #pr 10|Зоны Френеля\E #e [n=1;] _scom
Здесь снова вычисляется двумерный массив, но по оси Y всего 30 значений с более крупным шагом. И потом все 30 кривых рисуются. Интерес представляет только третья строка. Снова в переменных, обозначаемых заглавными буквами, надо определить 7 значений, а именно, начало числового массива, число точек аргумента, число кривых, начало и конец оси аргумента, номер первого цвета, остальные номера идут за первым и снова параметр, аналогичный (D) в прошлой программе, но теперь он в переменной (G). И точно такая же печать в текстовый массив.
Выше ничего не сказано о программировании, а просто представлены две суперкоманды, которые делают все, что нужно. По крайней мере для меня. На самом деле у этих суперкоманд есть код на языке ACL, и там можно увидеть много других команд, которые здесь не описаны. Лично я их уже больше не использую, а если кому интересно, то есть техническое описание, в котором описаны все тонкости и детали каждой команды. Вот ссылка . Вместе с тем далее в главе 12 будет описан пакет графики и там представлены две программы с более широкими возможностями. Одна из них рисует плоский рисунок в прямоугольнике осей координат. Но кривые могут иметь разные аргументы и не обязательно с постоянным шагом, а также могут изображаться маркерами, а не только линиями.
Вторая дает возможность рисовать двумерные зависимости как аксонометрическую проекцию поверхности в трехмерном пространстве с устранением невидимых линий. Кроме этого можно еще рисовать систему графиков со сдвигом осей и с устранением невидимых линий. В комплект для скачивания вместе с ПИ входит большой набор готовых программ, которые все это показывают, а код этих программ легко читается. Но я уже редко их использую, так как они искажают пропорции и дают неполную информацию. Все это делается в виде рекламы и чтобы было красиво. Но для работы это неудобно. Впрочем кому интересно, могут сами посмотреть готовую программу демонстрации научной графики. Сейчас взяли моду делать аксонометрию с расцветкой разными цветами разных высот. То есть как бы цветная карта, но с высотой. Либо высоту и проекцию одновременно. Но все такие картинки все равно искажают размеры. Когда то и я этим увлекался. Но со временем понимаешь, что не все то золото, что блестит.
Впрочем 3D моделирование и в самом деле очень сильно развивается, но для показа реального мира в компьютерных играх и макетах разных приборов или даже просто для виртуальной реальности. То есть нарисованного кино. И очень неплохо получается. Но это уже не наука. Это просто виртуальный мир. И это находится за пределами моих интересов и моей программы. Кроме того, есть большой набор уже готовых и бесплатных программ, которые все это делают. Гораздо интереснее познакомиться с возможностью анимации в языке ACL. Об этом в следующей главе.
7. АНИМАЦИЯ.
Плоские картинки -- это то, что могут видеть наши глаза в один момент времени. И то, что способен показать экран ноутбука. С точки зрения многомерности мира, в котором мы живем, это очень мало. Но компьютер вполне способен освоить и время как дополнительную ось координат. В жизни время -- это нечто большее, чем просто показать какую-то зависимость. Все процессы происходят во времени одновременно. Они могут пересекаться или быть независимы, не знать друг о друге. В масштабе космоса и релятивистких скоростей время -- это вообще очень сложно. В бытовом плане время дает нам кино.
Программирование освоило управление временем сразу же, как только появились экраны дисплеев. Грубо говоря, техника тут такая. Картинку можно рисовать сразу на экране, а можно виртуально, то есть в памяти. Ведь экран тоже в каждый момент показывает определенный участок памяти компьютера. Это все та же числовая матрица, которая зажигает каждый пиксель экрана так, как записано. Но рисование картинки может занимать какое-то время и вот это надо скрыть. Поэтому картинку рисуют в памяти, а потом в какой-то момент мгновенно копируют на экран. И получается как в кино, когда кадр стоит неподвижно 1/24 часть секунды, потом мгновенно меняется на другой и так далее.
Но на компьютере не обязательно делать такую маленькую паузу. Ее можно делать любой. В кино такое маленькое время паузы необходимо для показа движения. Просто человек не способен заметить такую маленькую паузу, мозг интерполирует картинки в непрерывный процесс. Но есть еще показ слайдов. Когда картинки тоже меняют, но не так быстро. И они могут быть разными. Анимация на компьютере дает и то, и другое. И кино, и слайды. Все зависит от того что и как показывать.
Наиболее легко на ACL можно сделать анимацию показа двумерного массива. Для этого надо три оси координат, две для аргументов и одну для функции. Выше было показано, что на картинке можно точно разместить две оси аргументов, а вот ось функции заменить цветом. Это работает и что-то показывает. Но функция получается не очень точно и не очень наглядно. А есть другой вариант. Показывать ось первого аргумента, ось функции, а ость второго аргумента заменить на время. В этом случае двумерный массив будет показывать изменение во времени зависимости от первого аргумента. Такую анимацию на ACL делать особенно легко, потому что есть готовая суперкоманда. Ниже я покажу работающий код программы. который показывает все тот же массив, что и раньше, но совершенно другим способом.
# nx=300; ny=300; n=nx*ny; J=101; j=J; y=0; d=0.02; #rep ny # y2=y*y; x=0;
#rep nx # a=sin(x*x+y2); r(j)=a*a; j=j+1; x=x+d; #end # y=y+d; #end
#d 17 r(1) 300 300 -1 1 -1.1 1.1 -1 0.5 4 0 1 0 0.25 4 1 J 1 #pr -|Зоны Френеля\E #e [n=20;] _scom
К сожалению показать анимацию на картинке не получается. Надо записывать видео. Какое-то время назад я записал видел другого двумерного массива, который считается более сложным образом. Но там используется та же суперкоманда с номером 20. Вот ссылка на это видео . Эта суперкоманда берет 17 значений входных параметров из первых элементов массива r() и из двух текстов последней печати, разделенных символом вертикальной черты. Числовые значения означают следующее: число точек по первому и второму аргументам функции, первое и последнее значения первого аргумента, начало и конец оси первого аргумента, разметка оси первого аргумента (это 3 числа, значение первой длинной риски, шаг до следующей длинной риски и число коротких рисок между длинными), начало, конец и разметка для вертикальной оси, номер кривой, которая будет показана первой, индекс массива r(), начиная с которого записан двумерный массив и время паузы в единицах 0.1 сек. Если индекс массива r() (16-й параметр) равен нулю, то двумерный массив читается из файла. А в печати, как обычно, полное имя файла и заголовок графика.
Как видим, все просто и входные данные просто конкретизируют что и как показывать. Все остальное суперкоманда делает сама. Но надо знать как ей пользоваться, это ведь уже сложный прибор. Работает она так. Сначала она показывает первую кривую и стоит. Для запуска анимации надо нажать клавишу [Enter]. В процессе анимации над графиком появляется номер кривой. Когда все значения второго аргумента будут пройдены, все начнется с самого начала. Остановить анимацию можно нажатием любой другой клавиши. Самая длинная -- это пробел, так что, проще всего ее и нажимать. Выход из анимации делается кликом крестика в правом верхнем углу окна или нажатием клавиши [Esc]. Вместо клавиши [Enter] можно нажимать клавишу [Backspace]. Тогда анимация пойдет в обратном направлении. Есть и другие варианты управления. Но для этого разумно почитать на сайте про описание суперкоманды, ссылку я уже указал выше.
Итак, теперь ясно как пользоваться, а как это работает? Как в языке ACL это реализовано? Чтобы ответить на этот вопрос я покажу текст этой суперкоманды (animdep) и расскажу как она все это делает. Сначала текст.
#pro curv
# j=1+(k-1)*n; #pas 2 r(j+n) r(Q) #ma [op=fno; b=j; nx=n; ny=1; mo=1;] # M=r(j+n+1); #pas 2 r(Q) r(j+n)
#d 7 A j n 1 x y 247 1100 # I=int(G/1000); G=0.01*(G-I*1000); J=30*G; K=470*G;
#p [tw=980*G; th=500*G; wid=870*G; hei=430*G; xs=90*G; ys=50*G; bot=3*G; top=6*G; tsi=26*G;]
#p [b=A; le=0; mo=0; sty=1; nx=B; ny=C; sa=2; uni=P; msi=0;] #w [op=pf; file=here; n=0; c=1; col=F; tfo=3; tki=0;] D E
#ag [op=m; n=2; xs=0; ys=-13; wid=W; hei=H;] \Tc d\u32*2;k = \S k;\u32*2;Max =\G M;\E #rob [mo=1; le=e;] # &=s(2);
@
# o=s(109)-99; #pas 26 A r(o) #pas 26 a r(o+26)
# a=s(4); e=s(5); #te [op=find; b=a; le=e; n=1; c=124;] # b=i(1)-a; c=i(1)+1; d=a+e-c; s(2)=0; s=0; e=r(17)*100;
# n=r(1); m=r(2); N=n*m; W=980; H=500; x=r(3); y=r(4); k=r(15); i=r(16); P=o-13; Q=P+11; r(P)=1; #pas 10 r(5) r(P+1) # &=i<1;
#case 0 #io [op=rd; fir=r(1); n=N; mo=1; file=\Ta b\E le=0;] #end |
#case 1 #pas N r(i) r(1) #end |
#ag [op=o; wid=W+20; hei=H+46; xs=(s(106)-W)/2; ys=(s(107)-H)/2; file=nomusic;] -\E # &=0;
#case 0 #e _curv
_#case 40 # &=s; #case 0 # s=1; k=k+1; &=k-1; #case m # k=1; #end | #end | #end |
_#case 48 # s=0; #end |
_#case 10 # s=0; k=k+1; &=k-1; #case m # k=1; #end | #end |
_#case 8 # s=0; k=k-1; &=k; #case 0 # k=m; #end | #end |
_#case 39 # &=s; #case 0 # e=e/2; s=1; #end | #end |
_#case 37 # &=s; #case 0 # e=e*2; s=1; #end | #end |
_#case 38 # &=s;
__#case 0 # s=1; &=1;
___#case 1 # U=(k+1)
___#end
__#end |
_#end |
_# &=1-abs(s(2)-27)<1;
#end # &=12345;
#ag [op=c;] #ini #pas 26 r(o) A #pas 26 r(o+26) a
Как видим, текста не так уж и мало. Но если учесть, что программа делает весьма сложную работу, то и немного. В любых других языках его было бы намного больше. Начнем с начала. В программе есть кусок кода, который повторяется два раза. Чтобы его не повторять используется механизм процедуры. То есть часть текста помечается и ему присваивается имя. Это делает команда pro (procedure). Ее аргументом как раз имя и является. Можно сказать, что это ее первый аргумент. А вторым аргументом является весь текст программы до символа @. Этот символ в адресах почты называют собакой. А для меня это жирная точка. Что делает ПИ. Она второй аргумент не выполняет сразу, но запоминает. Как она это делает даже не важно. А вот другая команда e (execute) имеет аргументами названия процедур. И она их выполняет по условию. А если нужно всегда выполнять, то перед именем надо ставить знак подчеркивания, например, #e _curv. Такая команда реально присутствует в тексте основной программы 2 раза.
Что делает процедура? Легко заметить, что там вычисляются и определяются разные переменные и параметры. И потом используются две важные команды. Первую w мы уже обсуждали. Но она использует операцию [op=pf;], которую мы не обсуждали. Эта операция рисует плоские графики и она используется в суперкоманде с номером 1, которую мы обсуждали. Здесь тоже можно было бы поставить эту суперкоманду. Это возможно и это работает. Но это не сделано по той причине, что данная программа сама является суперкомандой и вызывать из нее еще одну суперкоманду как бы расточительно по ресурсам. Ведь каждый вызов суперкоманды запускает другую процедуру и делает какую-то работу. Все равно это все работает и мгновенно. Но бывают супер-быстрые анимации и тогда это станет тормозить.
По этой причине в программе анимации суперкоманды лучше не использовать, а просто скопировать их текст в этот файл. Что и сделано. Можно заметить, что параметр sa (save) равен 2. Это значит, что картинка не показывается. а рисуется в шкаф, в ящик номер 2. То есть полностью готовая картинка находится виртуально в памяти компьютера. И вот самая последняя команда в процедуре -- это ag (animation graphics). Она как раз и управляет анимацией. У нее есть несколько операций, но главных 3. Это открыть окно анимации [op=o;], сменить один кадр на другой [op=m;] и закрыть окно анимации [op=c;]. Названия операций происходят от слов open, move, close. Все команды языка пишутся латинскими буквами. В данном случае используется команда смены кадра. Параметр [n=2;] указывает какую картинку из шкафа надо показать вместо той, которая уже стоит. Остальные параметры и аргументы показывают куда картинку надо поставить и какие тексты написать в заголовке окна анимации. Точнее не написать, а переписать.
Я не буду рассказывать тут все детали, есть техническое описание этой команды. Мне важно показать принцип работы. О том как пишутся форматированные тексты и какие параметры что означают я уже не раз рассказывал выше. На этой же строке находится еще одна новая команда #rob [mo=; le=;]. Тут история более сложная. Первоначально я ее сделал как робот. Эта команда могла имитировать действия пользователя, то есть нажимать клавиши, двигать и кликать мышкой. Это иногда полезно для тестирования программ с интерфейсом, а также для демонстраций. Я все это сделал, и это работало в системе Виндовс. А потом мне пришлось работать в системе Юникс (Solaris) и там это не работало. И я решил это ликвидировать, потому что хотел, чтобы программы работали во всех системах одинаково, а это не получилось. И вообще такие операции не так безобидны.
Итак, я все выбросил, но команду оставил. И сейчас она делает совсем не так много. У нее нет операций, но есть модификации. Так при [mo=1;] она просто останавливает работу программы на заданное время, то есть делает паузу. Время измеряется в миллисекундах и определяется параметром [le=e;]. Это необходимо, чтобы анимация была похожа на кино. Если этого не сделать, то картинки будут мелькать так, что ничего не будет видно. Разумеется, что паузу можно делать и принудительно вычисляя что-то ненужное. Но тогда ее длительность будет зависеть от скорости процессора. Но самое главное в этой команде то, что она не просто делает паузу. Она делает паузу в данном потоке, тем самым давая другим потокам выполнить свою работу. То есть она уступает очередь и пропускает вперед тех, кто стоит сзади.
Это тоже важный и сложный вопрос и как бы сейчас не в тему. Я просто хочу сказать, что такая команда нужна для многих целей, не только для паузы. Но реально время паузы будет чуть больше, так как какое-то время уйдет еще на рисование кадра. В сложных случаях это может быть достаточно большое время. Но тут уж ничего не поделаешь. Код нажатой клавиши возвращается в переменную s(2) и в конце процедуры он передается в переменную &.
Рассмотрим теперь основную программу с самого начала. В первой строке после символа (@) запоминаются значения всех однобуквенных переменных. Параметр s(109) равен размеру массива r(). Вообще-то этот массив в конкретной версии ПИ фиксирован и не меняется. Но у меня есть несколько версий ПИ, где этот массив имеет разное значение. Это зависит от типа компьютера и типа виртуальной машины языка Java (JRE). Так для 32-битной JRE были ограничения на размер программы и нельзя было заказать очень большой размер, либо это надо было делать очень сложным образом. Для 64-битной JRE ситуация изменилась и размер программы может быть любым, но все зависит от размера оперативной памяти компьютера. Бывают задачи, когда нужен очень большой размер, а бывает, что и не нужен. Чтобы во всех версиях программа работала одинаково надо было знать размер этого массива. И данный параметр его дает. Значения всех переменных временно перемещаются в конец этого массива, чтобы запомнить их. Сама программа их испортит, а их потом надо восстановить.
Потом идет обработка напечатанной строки текста и числовых параметров. В частности параметр номер 16 перешел в переменную i и надо проверить ее на 0. Если она равна нулю, то массив берется из файла и записывается в начало. А если нет, то он пересылается в начало. Это происходит после того, как все значения оттуда уже обработаны. После этого открывается окно анимации. Окно можно открывать в любом месте экрана, но чтобы не добавлять параметров, в данном случае окно устанавливается в середине экрана. При этом используются параметры s(106) и s(107) в которых записаны ширина и высота экрана ноутбука, на котором программа работает.
Дальше открывается первый (основной) цикл анимации и показывается первый кадр, то есть запускается процедура. Если ничего не происходит, то есть ничего не нажато, то параметр s(2) сохраняет свое исходное значение 0, и ни одно из условий не выполняется. Цикл повторяется снова и снова и все время показывает один и тот же кадр. Пользователь видит одно и то же, но на самом деле этот кадр постоянно заново рисуется. В какой-то момент пользователь может нажать какие-то клавиши. Номер нажатой клавиши передается в переменную s(2) и потом в переменную &. Коды клавиш можно найти в описаниях системы. Их также можно получить чисто эмпирическим путем, иногда это бывает полезно. Я указал на них в техническом описании команды w.
Здесь используются коды 8, 10, 37-40, 48. Это [Backspace], [Enter], клавиши стрелок и [0]. Циклы удобно записывать с отступом, чтобы было легко видно начало и конец каждого цикла. Но при записи сайтов пробелы игнорируются и чтобы мне было легче писать я заменил два символа пробела на один символ подчеркивания. Он ничего не значит, просто указывает на отступ. При написании текстов эти символы лучше заменить на два пробела каждый. Я рассмотрю только варианты 8 и 10. В каждом из них переменная s обнуляется, это для нас ничего не значит, а переменная k уменьшается и увеличивается на 1 соответственно. И делается проверка на начало и конец числа точек второго аргумента. Если условие выполняется, то счетчик исправляется так, чтобы остаться в нужном интервале.
Важно, что если больше ничего не происходит, то параметр s(2) сохраняет свое значение и кадры постоянно меняются либо увеличиваясь, либо уменьшаясь. Раньше цикл работал в холостую, теперь он реально работает. Но стоит нажать любую другую клавишу, кроме упомянутых, все изменится и кадры снова перестанут меняться, хотя цикл так и будет продолжать работать. Это необходимо, потому что только при этом идут новые запросы на действия пользователя. Он постоянно спрашивает, получает отказ и спрашивает снова. А клавиша [Esc] имеет номер 27. И этот номер проверяется в конце тела основного цикла. Как только он сработает, цикл остановится. На самом деле программа еще сложнее. Она реагирует на клавиши стрелки и позволяет уменьшать или увеличивать время паузы, просматривать кадры пошагово, или по требованию конкретного номера. Все это тоже реализуется определенной игрой параметров и условий.
После цикла надо закрыть окно анимации, восстановить нормальную работу циклов и выключить музыку. Это делает команда #ini. Дело в том, что кадрами анимации могут быть и просто картинки, которые можно прокручивать под музыку. В данной версии музыка включается только в самом начале. Я делал вариант, когда музыка включалась при каждом кадре, то есть можно было делать речевые комментарии к картинкам. Но это оказалось очень сложно и сейчас этого нет. Музыка включается в начале и работает непрерывно в зацикленном режиме. Данная команда ее отключает. И последнее -- восстановить старые значения переменных. Сейчас и это я делаю несколько иначе, но раньше делал так, как тут показано. Это тоже работает.
Такая программа может быть весьма полезной как в работе, так и в презентациях во время докладов. Следует отметить, что язык ACL очень легко переписывается на другой интерпретируемый язык Javascript (JS), который работает в браузерах. И я некоторые ACL программы реально перевел на язык JS. В том числе и данную суперкоманду. Образец работы такой программы в интернете можно посмотреть по этой ссылке . В интернете не очень удобно использовать клавиатуру, так как много людей смотрят сайты на смартфонах, где нет клавиатуры, а клавиатура на экране мешает смотреть сайт. Поэтому я делаю нужные кнопки прямо на экране. Но программы в браузере нельзя использовать в работе, так как им запрещено использовать файлы. А без файлов работа не полная, более того, почти ничего нельзя сделать. Впрочем браузеры создавались только для того, чтобы показывать то, что можно смотреть. Возможно со временем это изменится, но пока так.
Недавно я сделал и более сложную суперкоманду, которая показывает трехмерные массивы. Ее номер 28. Там почти все так же, только картинки (кадры) представляют собой цветные карты двумерного распределения, а со временем меняется ось Z. Такая программа удобна, например, для анализа данных по томографии. В томографии записывают двумерные сечения трехмерного объекта из проекций при его вращении вокруг какой-то оси. Получают большой набор сечений в плоскости XY при изменении координаты вдоль оси Z. И вот как раз ось Z заменяется на время. При этом можно использовать всего один массив огромных размеров и просматривать весь образец в одном окне анимации. Правда современные томографы каждое сечение записывают в отдельный файл типа tiff, но вытащить данные и сделать трехмерный массив несложно. Сложнее то, что такой массив будет иметь огромный размер.
Ниже я покажу текст простой программы, которая сама вычисляет такой массив, но в простой форме. Двумерные массивы имеют размер 300*200 точек, и всего таких массивов 100, то есть 100 точек по оси Z. Если все перемножить получаем 6 миллионов чисел. В стандартном варианте ПИ задано 26 миллионов, то есть хватает. Но реально -- это очень маленькие сечения и число точек по вертикали (по времени) невелико. Разумеется массив можно увеличить, но все же пределы для увеличения не очень высокие и разумно использовать другие решения. Например, сразу показывать картинки сечений из файлов. Такую программу я тоже сделал на языке JS и на отлично работает. И все же вот пример программы
# n1=300; n2=200; n3=100; J=101; nn=n1*n2; nt=nn*n3; na=2*n1; C=0; #ma [op=vic; b=J; le=nt;]
# j=J; C=1; k=na; #rep n3 #ma [op=vic; b=j; le=k;] # j=j+nn; k=k+na; #end
#d 19 r(1) n1 n2 n3 0 1 0 0.5 4 0 1 0 0.5 4 1 J 1 0 -1 2 #pr 1.dat|пример\E #e [n=28;] _scom
Здесь впервые появилась команда ma, которая реализует векторные и матричные математические расчеты. Она имеет много операций. В частности операция vic (vector initialize constant) присваивает элементам массива r(), начиная с индекса [b] и числу элементов [le] значение переменной C. То есть полностью обнуляет массив. Затем в цикле n3 раз в каждой двумерной матрице присваивается 1 сначала только в первой строке, потом в первых двух, потом трех и так далее. Потом задаются входные данные для суперкоманды с номером 28 и выполняется сама суперкоманда. Для этой суперкоманды надо определить 19 чисел. Первые 3 -- это число точек по осям X, Y, Z. Следующие 5 -- это разметка оси X, то есть начало и конец оси, значение первой длинной риски, шаг до следующей риски и число коротких рисок между длинными. Следующие 5 -- то же самое для оси Y. Затем номер сечения, которое будет показано первым, начало массива r(), где записан массив, который показывается. Если 0, то данные берутся из файла. После этого время паузы в единицах 0.1 сек, номер палитры цветов для показа картинок, параметр нормировки (-1 если не делать, 1 если делать индивидуально для каждого сечения), и наконец коэффициент масштабирования. Если он равен 1, то одна точка равна 1 пикселю экрана. Если точек мало, можно задавать коэффициент больше 1.
Печать такая же, как и в предыдущей суперкоманде. Так сделано, что даже если файл с числами не используется, его все равно надо задавать, причем с расширением из трех символов. Это как раз можно и легко переделать, но пока так. Программа работает, я проверил. На картинке справа показано как это выглядит на экране в стационарном режиме. Первоначально весь кадр черный, только одна строка белая. Потом белого становится все больше и больше. Разумеется это только очень простая демонстрация. Нетрудно изобразить весьма замысловатые узоры, которые трансформируются сложным образом. Или какие либо реальные физические процессы.
Я просто замечу, что можно без труда сделать и совсем простую программу (суперкоманду), которая будет показывать картинки из файлов с определенной паузой. Более того, эти картинки можно просто накидать в какую-то папку и программа их оттуда возьмет. Все это мы уже рассматривали выше, а код самой анимации точно такой же. Но я не сделал такую программу просто по той причине, что я ее сделал сразу на языке JS для браузера. Ее можно посмотреть у меня на сайте. И там же показано как приготовить для нее входные данные. Дело в том, что с файлами на компьютере браузер не работает, но картинки показывает. И если они уже готовы, то такая анимация вполне работает.
В языке ACL есть также другая программа, которую я первоначально сделал полностью на языке Java, а потом в готовом виде включил в ПИ. Она просто вызывается по команде #ag [op=s;] FT, где FT -- это аргумент (форматированный текст). Этот аргумент должен указывать адрес файла с протоколом слайд шоу. То есть она показывает слайд-шоу с фасонными переходами между кадрами и под музыку. Входные данные для нее имеют относительно сложный вид и задаются в отдельном файле. Как все это делать написано в интернете, вот ссылка . Я ее написал давно, но сейчас проверил -- она отлично работает. Причем, что интересно, она работает даже с файлами, размещенными в интернете.
В последней версии ПИ включен файл протокола, с которым программу можно сразу запустить вот по такой команде
#ag [op=s;] File:\M pro/data/sky1.vks\E
Эта программа как бы сразу была нацелена на интернет, поэтому для нее надо задавать полные адреса файлов в формате интернета. Если они реально находятся в интернете, то адрес начинает с букв (http://...). А если на компьютере, то адрес начинается с указания на файл так (File:C:/папка/...). Так как наш файл находится внутри папки ПИ, то можно использовать команду \M , которая подставит адрес папки ПИ на компьютере, где бы он не находился. Это универсально, поэтому удобно. Для меня оказалось удивительным, что программа до сих пор работает с файлами в интернете. Дело в том, что за последнее время было введено много ограничений на возможности языка Java работать в интернете. Да и вообще сайты перестали подключать другие сайты, если они не находятся на том же компьютере (сервере). Но данная программа сразу нацелена на интернет и работает только с файлами картинок и музыки, поэтому ее запреты не коснулись.
Важное замечание !!! Выходить из анимации надо только по клавище [Esc]. Если просто закрыть окно, то музыка не выключится и будет продолжать играть.
Но не у всех быстрый интернет. Если интернет тормозит, то для просмотра презентации (примера) можно скачать папку [sky] на свой компьютер внутрь папки (C:/0/) (если ее нет, надо создать) из архива по этой ссылке . И потом поменять цифру 1 в аргументе написанной выше команды на цифру 0. И все будет работать на компьютере без интернета. Файлы с расширением vks -- это и есть протоколы. И по образцу можно сделать и собственное слайд-шоу. Лично у меня их много, а данный альбом был одним из первых.
В языке ACL также реализована еще одна любопытная анимация, которая тоже первоначально была сделана на Java, а потом из нее был выделен математический блок, а все остальное команды ACL делают достаточно быстро и намного проще, чем на Java. Эта анимация показывает движение кружков в замкнутой области. Кружки двигаются с разной скоростью, сталкиваются упруго между собой и стенками области и получается движение очень похожее на реальное, если бы такую систему удалось реализовать. Так как потери энергии при столкновении не учитываются, то процесс может продолжаться бесконечно долго. Обычно первоначально кружки покоятся и распределены равномерно. По команде одному из них дается толчок и он начинает толкать остальных. Что потом происходит описывается статистическими законами.
Я покажу одну из большого числа возможных реализаций этой программы. Несколько штук представлены в списке готовых программ с внешним видом и входными параметрами. Эта программа не самая простая, но и не самая сложная. Она показывает две прямоугольные области, разделенные узким проходом. Одна область заполнена кружками, другая пустая. В процессе движения некоторые кружки случайно попадают в проход и оказываются во второй области. Постепенно число кружков в каждой из областей выравнивается. Код использует уже уже описанные команды анимации, но сами картинки рисуются простым графическим пакетом Java, который полностью перенесен в ACL, только все записывается более компактно. О нем я, возможно, расскажу позднее. А сейчас обратим внимание только на анимацию и как она реализована. Итак вот полный код полностью работающей программы
# w=600; h=400; N1=6; N2=8; E=10; N3=1; R=10; S=22; W=w+50; H=h+40; V=sqr(E/N3); N=N1*N2; k=1;
#rep 200 # i(k)=155*rnd(0)+50; i(k+1)=155*rnd(0)+50; i(k+2)=155*rnd(0)+50; k=k+3; #end
#col [b=1; le=200; fir=i(1);] # D=2*R; D2=2*D; S2=S/2; w1=w/2-D2; w2=w/2+D2; h1=h/2+S2; h2=h/2-S2;
# w8=w/2/N1-10; h8=h/N2; y=h8/2; k=1;
#rep N2 # x=w8/2; #rep N1 # r(k)=x; r(k+1)=y; r(k+2)=0; r(k+3)=0; x=x+w8; k=k+4; #end # y=y+h8; #end
# j=2001; k=1; #rep N # r(j)=r(k); r(j+1)=r(k+1); j=j+2; k=k+4; #end
# k=3; #rep N3 # A=6.283185*rnd(0); r(k)=V*cos(A); r(k+1)=V*sin(A); k=k+4; #end
#d 9 i(1) 200 255 200 0 0 0 220 220 220 #col [b=201; le=3; fir=i(1);] # K=99999; N1=12;
#d 26 r(K) 0 0 0 h w1 h w1 h1 w2 h1 w2 h w h w 0 w2 0 w2 h2 w1 h2 w1 0 0 0
# j=1; i=K; #rep N1 # i(j)=r(i+2)-r(i); i(j+1)=r(i+3)-r(i+1); j=j+2; i=i+2; #end
#ag [op=o; wid=W; hei=H+26; xs=(s(106)-W)/2; ys=(s(107)-H)/2; file=nomusic;] Полный и пустой\E
#p [xs=0; ys=-13; tfo=3; tki=0; tsi=10; sty=2;] # &=0;
#case 0
_#g [op=open; twi=w; the=h; col=245;] #g [op=area; nx=r(K); ny=r(K+1); b=1; mo=0; col=246; n=N1;] # j=1; k=1; !
_#rep N # y9=r(k+1); #g [op=oval; mo=0; wid=D; hei=D; nx=r(k); ny=y9; col=j-int((j-1)/200)*200;]
__#g [op=text; ny=y9-4; col=202;] \I-2 j;\E # k=k+4; j=j+1; #end
_#g [op=clos; sav=2;] #g [op=open; twi=W; the=H; col=245;] #g [op=imag; nx=W/2; ny=H/2; n=2;]
_#g [op=clos; sav=1;] #ag [op=m; n=1;] Полный и пустой\E #rob [mo=1; le=1;] # &=abs(s(2)-10); !
_#case 0 #ma [op=bsm;] #ma [op=bsi;] #ma [op=bsr;] #end | # &=0;
#end #ag [op=c;] #ini
Если посмотреть что данная программа делает, то становится удивительно как такой сложный процесс можно запрограммировать таким простым и компактным кодом. И все таки. Начнем разбираться. В первой строке в переменные вводятся числа. Это входные данные. Смысл переменных такой: w, h -- ширина и высота прямоугольной области, N1, N2 -- число кружков по горизонтали и вертикали, E -- энергия движения, N3 -- число кружков, получающих энергию в самом начале, R -- радиус кружков, S -- толщина узкого прохода. Дальше определяются нужные размеры, энергия пересчитывается в скорость на один круг, определяются первые 200 цветов для кружков случайным образом. Затем для всех кружков определяются из начальные координаты. Первым выделенным кружкам сообщается одинаковая скорость по величине и случайная по направлению. В специальную область массива r() вводятся входные данные для математических расчетов. Это все предварительные приготовления.
И вот начинается самое главное. Открывается окно анимации командой #ag [op=o;]. Определяются параметры, которые не меняются в цикле. И открывается цикл. Уже в цикле рисуется картинка с помощью команды #g. Эта команда открывает область рисования, рисует области, все кружки и номера на них. Все в цикле. Потом рисование закрывается и картинка спасается в шкаф с номером 1. Затем показывается кадр анимации с номером картинки и ставится минимальная пауза. В этой анимации, если поставить маленькую энергию ничего мельтешить не будет, так что задерживать не обязательно. После этого делается проверка на то какая клавиша была нажата последней. Если не [Enter], то ничего не делается и ничего не происходит, картинка все время одна и та же.
Но стоит нажать клавишу [Enter] и запускаются три специальные операции команды математических расчетов. Они вычисляют новые координаты и скорости всех кружков с учетом их соударений между собой и со стенками. Это очень сложные расчеты и на языке ACL они будут выполняться очень долго. Поэтому они сделаны сразу в виде команд и выполняются ПИ. После пересчета картинка каждый раз будет меняться. И так до тех пор пока не нажать любую другую клавишу. Тогда процесс снова остановится, потому что пересчета не будет. Вот казалось бы и все.
Но ведь нет. Ведь видно, что выйти из цикла никак невозможно. Цикл бесконечный. Да, так и есть. Здесь не сделан выход их цикла по клавише [Esc]. И по правилам программа не сможет закончится. Фокус в том, что в команде анимации специально сделан такой режим, что если закрыть окно анимации крестиком, то такое событие блокирует все циклы и они перестают работать. И поэтому программа все равно выйдет из цикла. Но потом надо обязательно поставить команду #ini , которая восстановит нормальную работу циклов. Частично так сделано как раз потому, что очень легко забыть предусмотреть выход из цикла именно в таких программах. И тогда возникает неприятная ситуация и приходится снимать задачу сложным и принудительным методом. А для новичков это вообще трагедия.
Но при работе в таком режиме нельзя включать музыку. Музыка не имеет отношения к окну анимации и она не выключится. Интересно, что на ACL очень легко и просто нарисовать сложные области фасонного типа и вообще программу с внешним видом и интерфейсом для задания параметров. Всего это намного проще, чем на Java. А на Java нужно приготовить только блок математических расчетов, которые долго считаются. Это общий принцип взаимодействия кода на языке Java и на ACL. Справа я показал две картинки, какие дает эта программа в самом начале и в процессе.
До сих пор компьютер проверял действия пользователя только при показе очередного кадра. Но бывают анимации с длительной паузой. И тогда реакция на действия пользователя будет происходить с большим опозданием. Это неудобно. Поэтому разумно паузу делить на мелкие части в цикле, а между ними проверять действия пользователя. Такую проверку позволяет выполнить команда #ag [op=p;]. Эта команда используется в программе тренажера визуальной памяти, где игроку показывают картинку, потом разрезают ее на много частей и части перепутывают. И игрок должен путем парных перестановок восстановить картинку. И еще одна команда #ag [op=i;], наоборот, обнуляет все действия пользователя и возвращает взаимодействие в исходное состояние. Иногда это тоже необходимо.
Несмотря на простоту и, казалось бы, неразвитость механизма анимации, он позволяет делать много интересных приложений. Все зависит от фантазии программиста. В него можно подключать как сложную графику, так и сложные математические расчеты, работу с файлами и многое другое. Можно просто показывать динамику очень долгих вычислений. Для этой цели в языке есть также готовая команда, которая называется pf (progress form). Она тоже имеет три операции (o, m, c) и просто показывает степень выполнения работы путем закрашивания пустой ленты цветом. Это тоже анимация, только очень специальная. Такую команду удобно ставить в циклах. Перед циклом ставим операцию [op=o;] и указываем сколько в цикле повторений. В самом цикле ставим [op=m;] и указываем счетчик цикла, который все время расчет. А после цикла ставим [op=c;].
8. МАТЕМАТИЧЕСКИЕ ВЫЧИСЛЕНИЯ. С ЧЕГО ВСЕ НАЧИНАЛОСЬ.
Я сознательно начал рассказывать с таких вещей, с которыми сразу сталкивается начинающий пользователь современного ноутбука. Но самые первые компьютеры всего этого не умели. Их главной задачей было проводить математические расчеты, потому что без компьютеров это делалось невыносимо долго и работа была крайне не интересной. Именно способность компьютера быстро делать вычисления вывела человечество на новую ступень развития, когда стали возможны полеты в космос и автоматические заводы, не говоря уже про искусственный интеллект.
Во всех приведенных выше примерах вычисления тоже проводятся на чисто интуитивном уровне. Но пора разобраться с этим более основательно. Для вычислений используется модель из двух компонентов: память и процессор. В памяти находятся числа, в процессоре из одних значений получаются другие. Процессор работает по программе. Но не по той, которую пишет пользователь на каком-либо языке, например, ACL, а по более примитивной программе. Есть разные способы, но я рассмотрю один из самых первых. Каждая команда такой программы имеет 4 числа. Первое число -- номер операции, второе число -- первый операнд, третье -- второй, четвертое -- результат. Операнды и результат -- это просто адреса памяти, в которой есть очень много пронумерованных ячеек, в каждой одно число.
Это тоже условно, так как реально числа имеют разные типы и могут состоять из многих компонентов. На самом низком уровне в компьютере есть всего два числа. Это 0 и 1. Больше никаких чисел нет. И вот из этих двух чисел путем их комбинирования можно получить весь наш сложный мир со всем его многообразием. А в языках высокого уровня все это многообразие представлено. Есть много типов чисел, которые можно объединять в произвольные массивы и так далее. Мне это не нравилось с самого начала и я от этого отказался. А в самом начале я работал на таких компьютерах, где ничего этого не было. Я оставил только 4 типа чисел, плюс специальный массив служебных чисел, которые сами в вычислениях не участвуют, но регулируют процессы. Первый тип чисел -- это переменные. Это, если говорить точнее, не числа, а ящики для чисел. Они могут менять свое содержание, но там всегда есть всего одно число. Переменные имеют имена, но это все равно элементы массива и можно это использовать если знать кто за кем идет.
При этом в языке ACL имена переменных не могут быть произвольными. Порядок такой -- сначала идут строчные однобуквенные переменные от a до z, потом прописные от A до Z, и наконец переменные с именами $, %, &. Всего их 55. Они образуют первый массив. Второй массив имеет те же самые переменные сначала с цифрой 0, потом 1 и так далее до 9. Всего их 550. Наконец, третий массив имеет двухбуквенные переменные от aa до &&. Всего их 3025=55*55. Третий массив появился сравнительно недавно, а именно 21 июля 2020 года. Также есть один целый массив i(149999), один вещественный массив r(25999999) и один символьный (текстовый) массив t(1999999). Индекс элемента массива указывается в круглых скобках. Я указал максимально возможный индекс элементов массивов, а минимальный всегда равен единице. Дополнительно есть служебный массив целых чисел s(112). Это тот самый массив, некоторые элементы которого имеют имена и называются параметрами. А некоторые элементы этого массива используются без имени, хотя и именованные элементы тоже можно использовать таким образом.
Вот такая простая память. И все жестко фиксировано. То есть все процедуры и все команды всех программ используют одну и ту же память и надо следить за тем, чтобы новые процедуры или команды не портили память, которую раньше использовали старые команды. Это минус, тот факт, что надо следить. Как раз в языке Java есть разные типы памяти, общая, типа той, что у меня, и локальная, которая используется только в пределах данной процедуры. Это как бы удобнее, потому что не надо следить. Но приходится вводить аргументы у функций и расписывать типы и следить за ними. Лично мне это не нравится. Лучше следить за порчей памяти, чем писать много лишних слов. Хотя следить надо и очень внимательно. Ошибки такого типа приводят порой к парадоксальным результатам.
Так вот, процессор компьютера выполняет только операции типа d=a+b; Здесь a и b есть операнды, + есть операция, d есть результат. Все скобки и прочие конструкции развертываются в такие операции на стадии компиляции или интерпретации кода программы пользователя. Это кажется сложным, но если знать алгоритмы, то не так уж и сложно. А память компьютера -- это всего один массив, если иметь в виду оперативную память. И этот массив сложным образом разделяется на блоки, группы и так далее. Но есть еще и внешняя память, которая может быть разной, то есть встроенный винчестер, внешний винчестер, флешки и так далее. Главная сила компьютера в том, что он может производить однотипные вычисления в цикле, то есть повторять много раз.
А специфика интерпретируемых языков в том, что они должны постоянно расшифровывать код пользователя, то есть доводить его до уровня, понятного компьютеру. И иногда на эту расшивровку уходит больше времени, чем на сами вычисления. Но это совсем не страшно, если вычисления делаются один раз, или мало раз в цикле. А вот если много раз, то тогда интерпретируемый язык будет работать во много раз медленнее. чем компилируемый язык, который эту операцию проводит заранее, до выполнения циклов. Бывают интерпретируемые языки, которые циклы все же сначала компилируют, потом выполняют. Таким является Java. А если этого нет, то надо избегать делать циклы. То есть циклы должны быть внутри команд языка.
Если циклы внутри, то они тоже будут компилироваться и не будут тормозить. А расписывать надо только одноразовые вычисления. Для этих целей сделана команда ma (mathematics). Она имеет много операций, как примитивных так и сложных. К примитивным относится инициализация массивов, простые арифметические действия, функции. Но могут быть и сложные вычисления, в которых есть циклы. Рассмотрим пример. Нам надо обнулить 99999 самых первых элементов массива r(). Это очень просто записать так
# j=1; #rep 99999 # r(j)=0; j=j+1; #end или так # C=0; #ma [op=vic; b=1; le=99999;]
У второй записи есть два преимущества. Во-первых, она просто короче и понятнее читается при определенном навыке. Но самым главным является ее второе преимущество. Она будет намного быстрее давать тот же самый результат. Потому что у нее нет цикла. Ничего повторять не надо. Цикл будет делать ПИ, а она работает намного быстрее. И чем больше повторений, тем быстрее она будет работать. Я не стану тут расписывать все многообразие операций, какие есть у команды #ma. Все это написано в техническом описании по ссылке . Я просто хочу отметить, что эти команды для своей работы могут использовать информацию через параметры, но это целые числа, а реальные числа берутся из переменных. Например, команда
# C=0; D=1; #ma [op=via; b=1; le=99999;]
инициирует массив арифметической прогрессией, у которой первый элемент равен 0, а каждый следующий на 1 больше. Так же точно можно вычислять функцию Гаусса и другие функции. Тут как бы все понятно и нет проблем. Таких операций можно сделать столько, сколько нужно, чтобы не связываться с массивами. Так же точно можно проводить операции над двумя массивами. Обычно я предпочитаю изменять первый массив, это получается экономнее. Если его не нужно изменять, то его можно скопировать в другое место. Тут может возникнуть путаница. Реально у меня определен только один массив r() для вещественных чисел из 8 байтов. Но любые части этого массива -- это тоже массивы, просто меньшей длины. Их можно различать по индексу первого элемента и длине. Обычно они указываются параметрами [b] и [le]. Для копирования таких массивов сделана другая команда #pas n r(J) r(K). У этой команды три аргумента -- число элементов, первый элемент первого массива, первый элемент второго массива.
Можно делать копирование одного типа массива в другой тип. И даже в переменные. Как я уже сказал, переменные тоже организованы в массивы, но надо знать структуру этих массивов. Она указана выше. Команда pas копирует только массивы. А иногда удобно делать пакетные задания значений. Почему-то в других языках я этого не видел. Для этой цели я сделал две команды. Первая имеет вид #d 5 r(J) a*2 b c d, вторая #v 5 r(J) a e b c d. Первая d (data) определяет значения массива из переменных, причем вместо переменных могут быть и числа. Вторая v (value) делает обратную операцию, то есть передает значения из массива в переменные. Во второй команде нельзя писать числа и повторения. То есть формально повторения без знака * писать можно, но это неразумно. Операции над двумя массивами сделаны так
#ma [op=vvm; b=1; le=999; trx=999;]
тут операция vvm означает умножение вектора на вектор (vector vector multiplication). Есть и другие операции. Оба массива должны иметь одинаковую длину, первый начинается с 1, индекс второго сдвинут относительно первого на trx=999. Первый массив получает результат, то есть портится. То есть это аналог операции a=a*b; Вообще говоря, математику можно было бы сделать компактнее. И в других языках (Питон, Матлаб) так и сделано. Но я не стал так делать, потому что массивы все равно надо где-то определять, и лучше уж все вместе. Это вовсе не минус. А вот реальным минусом языка ACL является отсутствие комплексного массива и комплексных вычислений. Нельзя сказать, что они совсем отсутствуют. Они, конечно, есть. Просто не совсем компактно и наглядно описываются. Но об этом позже. А пока посмотрим что с матрицами.
А ничего особенного. Все матрицы -- это тоже части массива r(). Просто вместо параметров [b] и [le] они определяются параметрами [b], [nx] и [ny]. При этом сначала записываются все значения первого индекса при первом значении второго, затем то же самое при втором значении второго и так далее. Это можно себе представить как картинка разматывается по строкам снизу вверх. Кстати именно такое соответствие между матрицами и картинками используется в ACL. Хотя принято картинки рисовать сверху вниз, то есть первая строка наверху. Очень часто приходится делать операцию транспонирования матриц, она выглядит так
#ma [op=mtr; b=1; nx=200; ny=2;]
Операций с матрицами в ACL много. Матрицы можно складывать, нормировать, вращать, вырезать части, заполнять фрагментом и много чего еще. Ведь операции над матрицами эквивалентны операциям над картинками. Есть даже операция поиска максимума в матрице и полуширины по двум направлениям. Когда операций не хватает, легко сделать еще одну. И вот теперь удобно перейти к комплексным вычислениям. С точки зрения записи комплексных чисел, они представляют собой массивы, у которых первый индекс имеет два значения. Если транспонировать такую матрицу, то мы получаем сначала все реальные части, потом все мнимые части. Это уже просто два реальных массива. С ними можно работать как с векторами.
Я сделал операции сложения и умножения комплексных векторов и матриц, а также другие операции типа быстрого преобразования Фурье. Сложнее работать с комплексными переменными, так как не очень удобно расписывать все операции, даже элементарные. Хотя на скорость вычислений это не влияет, но просто неудобно записывать. И я сделал аппарат записи команд как в примитивных языках и как раньше работал компьютер. Такая операция называется
#ma [op=com; em=0;] K A B C K A B C . . . или #ma [op=com; em=1; b=11;] + a b c / a b c . . .
Фактически тут две разновидности этой операции. В первой (она была раньше) все записывается числами, причем K -- код операции, A, B -- номера операндов, C -- номер результата. Реализованы следующие коды операций: 1 - сложение, 2 - вычитание, 3 - умножение, 4 - деление, 5 - exp(A), 6 - cos(A), 7 - sin(A), 8 - tan(A), 9 - pow(A,B), 10 - log(A), 11 - J0(A), 12 - J1(A). Для функций второй операнд не используется, кроме возведения в степень, в ней используется только реальная часть второго операнда. Интересно, что есть вычисления функций Бесселя от комплексного аргумента. Во второй записи надо все комплексные переменные разместить в массиве r() плотно и указать начало размещения, которому ставится в соответствие латинский алфавит и операции указываются их символами, а операнды буквами латинского алфавита. Так немного нагляднее. Второй вариант был сделан позднее. Те же самые операции тут обозначаются так ( + - * / E C S T P L 0 1 ). Более точную и подробную информацию можно получить в техническом описании.
Впрочем надо сказать что операцию умножения комплексных матриц я сделал недавно и в этой же команде. Она выглядит так
#ma [op=com; em=2; b=11;]
где параметр [b] указывает на первый элемент целого массива i(), в котором надо записать 6 целых чисел: i1 i2 i3 n1 n2 n3. Они означают следующее. i1 -- это начальный индекс реального массива r(), где записана первая матрица. i2 -- то же самое для второй матрицы. i3 -- адрес реального массива, где будет записан результат. Исходные матрицы и результат не должны пересекаться. Далее n1 -- это число строк первой матрицы, n2 -- число столбцов первой матрицы, вторая матрица имеет число строк, равное n2 и число столбцов n3. В частном случае эта операция позволяет умножать комплексный вектор на комплексное число, если размерности равны n 1 1. Или можно сделать матрицу из двух векторов при n 1 m.
Тут уместно отметить, что иногда бывает удобно просто все математические расчеты выполнить на языке Java в виде процедуры, а саму процедуру вызывать в языке ACL в готовом виде через команду вызова процедур. Такие команды я стал вызывать по номеру после символа \. Было много вариантов и все они описаны. Но последнее время я развиваю только процедуру \10. Про нее написано в отдельном документе, вот ссылка . В старых ACL программах можно увидеть вызов и других процедур такого типа. Они тоже имеют описание. Но лучше пользоваться новой. Надо сказать, что программировать вычисления на языке Java относительно просто, и я разработал механизм, когда такие куски кода можно компилировать отдельно от основной программы и потом скомпилированный код можно просто вставить в ПИ файл, после чего он будет использоваться в ACL как почти родная процедура. Об этом тоже написана отдельная статья, вот ссылка . Правда в этом случае надо скачивать компилятор языка Java. В статье написано как это сделать.
9. РАБОТА С ФАЙЛАМИ И ФОРМАТЫ ДАННЫХ.
Файлы, так же как экран и клавиатура, появились не сразу. Первые 20 лет (70-е и 80-е годы прошлого века) я работал на компьютерах без всего этого. Тогда компьютеры были очень большие и общие, мог быть один компьютер на всю организацию. Для пользователей он работал по ночам, а днем его постоянно тестировали и чинили, потому что он часто ломался. Код программы и входные данные он получал на перфокартах, а результаты печатал на бумагу. Перфокарты сдавали и бумагу получали в специальном окне. Каждый пользователь имел свой номер. Мой номер был 347, его надо было писать на обложке колоды перфокарт. И по нему получать результат.
Рядом с этим окном стоял огромный железный мусорный бак. Очень часто люди получали толстую пачку крупных листов бумаги, просматривали ее тут же, и сразу выбрасывали в этот бак. Они заметили в программе ошибку, и результаты не имели никакого смысла. Запустить программу в работу можно было только один раз в день. И любая ощибка отодвигала момент решения задачи на один день. Современному человеку со смартфоном невозможно это даже представить. Это было реально первобытное время. Но именно тогда были придуманы все основные языки программирования и все алгоритмы решения математических задач.
Файлы появились вместе с персональными компьютерами. Точнее чуть раньше, но раньше не для всех. И они сейчас являются основой не только работы на компьютере, но и интернета. Ведь весь интернет -- это просто океан файлов, в котором каждый файл, как капля. В файлах записана информация, которая не исчезает, может долго храниться. Но главное даже не это. Файлы можно легко копировать, ими можно обмениваться и значит их невозможно уничтожить. Они размножаются как вирусы. Единственное, что может уничтожить файлы -- это потеря интереса к ним. То есть появление более интересных файлов.
В процессе своей работы программа должна уметь читать информацию из файлов и записывать ее обратно в файлы. Уже не нужна бумага ни на входе, ни на выходе. А размеры носителей файлов становятся все меньше. Уже сейчас маленький квадратик с ноготь пальца может хранить все книги районной библиотеки. Конечно предел есть. Наверно 0 или 1 в размер меньше одного нанометра записать не получится. Даже атомы имеют конечный размер. Но кто знает, ведь есть еще свет, есть квантовая механика. Неясно, что будет в будущем. А пока надо понять как эти файлы записываются и что в них можно записать.
Понятно, что в файлы записывают то, что хранится в оперативной памяти компьютера, пока он включен. Но это не совсем так. Компьютер работает с данными и его задача все это делать быстро. В нем данные находятся в таком виде, чтобы ими можно было быстро воспользоваться. Назовем этот вид raw (сырой, необработанный). А задача записи в файлы совсем другая -- записать как можно компактнее. Тут скорость не важна, важен размер числа нулей и единиц. Чем компактнее запишем, тем больше сможем записать. Поэтому данные перед записью часто кодируются с целью уменьшения размера (сжимаются). Способы сжатия могут быть разными. Это тоже наука, точнее технологии. И программисту приходится все это знать и понимать.
Начнем с этим разбираться. Я уже немного говорил об этом в связи с записью картинок. Но начинать надо все-таки с чисел. Это главное. Картинки в конце концов -- это просто числовые матрицы. Как и тексты книг, и музыка. Это все можно записать числами. Исторически так сложилось, что числа стали группировать по степени числа 2. Два числа 0 и 1 можно группировать по разрядам. Один такой разряд назвали битом. Все таки 2 -- это очень мало. Хотя бывает, что и достаточно. На многие вопросы есть всего два ответа -- Да и Нет. То есть логика вполне может оперировать с битами. Как и книги. Там точка либо черная, либо белая. И этого достаточно. Но часто все-таки этого мало. И за основу на следующем этапе сложности выбрали 8 разрядов. 2 в 8-й степени -- это 256. Группу из 8 битов назвали байтом. В одном байте можно записать целые числа без знака от 0 до 255 или со знаком от -128 дл 127. При этом запись устроена таким образом, что отрицательные получаются из положительных вычитанием 256. А реально отрицательные числа больше положительных.
И очень многое на первом этапе развития персональных компьютеров записывалось в байты. И до сих пор это сохраняется. Так компьютеры часто используют 256 цветов, или 256 градаций красного, зеленого и синего в максимальном количестве цветов 16777216. Базовое число символов текста, которое способен использовать компьютер тоже первоначально равнялось 256. При этом первые 128 были одинаковы для всех, а вот вторые обычно содержали символы конкретного языка конкретной страны. Поэтому существовали и до сих пор существуют разные кодировки, причем разные даже для одного языка. Например, для русского языка есть три кодировки. Но сейчас уже существует и двухбайтовая система символов, единая для всех стран, куда записали символы всех языков и появилась возможность писать на многих языках сразу. Они называются юникодами, а первые ascii кодами. Раньше такой возможности не было.
Хотя все это как-то регулируется, но все равно многое происходит случайно, по принципу, кто успел, тот и съел. Кажется уже и двух байтов не всегда хватает для записи символов. Важен также порядок, то есть какие символы в какое место очереди попали. Потому что шрифты до сих пор делают не для всех символов. Формально символы есть, но некоторые шрифты вам их не покажут. Про то как записываются ноты я ничего не знаю. А про то как записывают картинки я уже немного рассказал. Но вернемся снова к числам.
В моем языке ACL есть только целые знаковые числа длиной 4 байта и реальные числа длиной 8 байтов. И все. Это сегодня самые массовые форматы чисел и их достаточно. Но файлы записываются в более широкий набор форматов, и их надо уметь читать и уметь в них записывать. Поэтому при чтении чисел из файлов и записи чисел в файлы такие форматы используются. Также числа часто записываются просто текстом, то есть реально символами десятичной системы счисления. Для работы с файлами в языке ACL есть две команды. Первая называется io (input, output), вторая просто f (file). Как раз первая читает и записывает данные. А вторая файлы преобразует из одного вида в другой или выполняет с ними другие операции.
Кстати операционные системы на компьютерах первоначально появились как раз для работы с файлами. То есть команда f тесно взаимодействует с операционной системой. И благодаря ей, программа на языке ACL способна делать такую же работу, как и операционная система. Но сначала все же про команду io . Ее общий вид такой
#io [op=; fir=; n=; file=; fo=; mo=; le=; ord=;] причем op = rf wf rb wb rd wd rt wt
Это вполне компактная запись, учитывая многообразие возможных вариантов. Названия операций состоят из двух букв. Первая буква имеет два значения: (r), то есть read, означает чтение из файла, (w), то есть write, означает запись в файл. Вторая буква указывает на формат записи. При этом (f), то есть format, означает запись и чтение чисел текстом по определенному формату. При этом используется параметр [fo] (то есть format). Буква (b) (то есть byte) означает чтение и запись байтов как целых знаковых чисел. Буква (d) (то есть data) означает запись чисел как данных в компьютерном коде и разных модификациях. При этом используется параметр mo (то есть mode). Обе буквы (b) и (d) при чтении используют параметр [le], который указывает сколько байтов от начала файла надо пропустить прежде, чем начать читать данные. Наконец буква (t) (то есть text) означает запись текстов. При этом используется только символьный массив, а запись идет специальным образом. Тексты также можно записывать и считывать побайтно по букве (b).
Теперь нужно объяснить какие есть форматы при записи чисел текстом. На самом деле их немного. При чтении автоматически читаются все известные форматы и параметр [fo] используется только для того, чтобы указать сколько строк текста надо пропустить прежде, чем начать читать числа. Это делается записью типа *5. Символ * указывает на то как надо понимать число 5. Важно, что в этом случае байты никакого значения не имеют, пропускаются именно строки, то есть куски текста, которые заканчиваются юникодом 10. А при записи чисел есть всего два формата. Первый -- это формат \G команды #pr. Ее мы рассмотрели в самом начале статьи. И здесь в параметр [fo] тоже надо записать такую же запись *5, только теперь число после символа * означает сколько чисел надо записать на одной строке.
А второй формат имеет вид [fo=EN.M.L;], например [fo=E10.12.5;]. При этом первое число N указывает сколько чисел надо напечатать на одной строке (как и в первом случае), второе число указывает сколько символов надо отвести на одно число (в первом случае оно фиксировано и равно 10) и третье число указывает сколько символов надо отвезти на дробную часть числа ( в первом случае оно фиксировано и равно 4). Но есть еще одна разница между этими двумя случаями. Формат \G пишет числа так -2.3456-23, а второй формат так -2.3456E-23.
Отличие в том, что перед показателем степени во втором случае ставится символ E, от которого я отказался. Поэтому, если вы работает только на языке ACL, то программа при чтении поймет любую запись. А вот другая программа первую запись не поймет, так как стандарт -- писать символ E перед показателем степени. Как раз для взаимодействия с другими программами и был введен второй формат. Форматов можно было бы сделать и больше, но в этом нет необходимости. Любой фасонный формат можно сделать с помощью команды #pr и потом просто записать вместо чисел текст. Просто иногда удобно записать числа с помощью этой команды, это будет быстрее и проще. Но если нужно фасонно, то тогда лучше все писать текстом.
Перейдем к объяснению типов данных. Тут расклад такой. При [mo=1;] числа записываются и считываются в формате float (4 байта на число). Для построения графиков и картинок этого вполне хватает. Это самый массовый тип записи, поэтому он первый. При [mo=2;] используются только знаковые целые числа и записываются в 4 байта, как в массиве i(). При [mo=3;] используются реальные числа и записываются в 8 байтов, как в массиве r(). Если запись делается для продолжения расчета то надо записывать именно так. При этом точность расчетов не теряется. При [mo=4;] используются только знаковые целые числа и записываются в 2 байта. При [mo=5;] используются только целые числа без знака и записываются в 2 байта. И вот в этом месте нужно указать на еще одну особенность таких операций.
Когда числа записываются в несколько байтов, то важен порядок записи байтов. Так сложилось исторически, конкретных причин я точно не знаю, хотя догадки есть, что система Виндовс записывает числа младшими байтами вперед. А система Юникс записывает в обычном порядке, сначала старшие байты. В Java, а значит и в ACL используется запись как в Юникс. По этой причине числа, записанные программой на Java, не читаются в программах, написанных для системы Виндовс. И наоборот. Надо переворачивать порядок байтов. Однако при [mo=5;] я сделал так, что порядок байтов может быть любым. Он определяется параметром [ord]. Если [ord=0;], то порядок как в Java (Юникс), а если [ord=1;], то как в Виндовс. Эта модификация была сделана для чтения графических файлов типа tiff, которые могут записывать картинки двухбайтовыми целыми числами без сжатия и с любым порядком байтов.
Вообще говоря, в ACL можно сделать операции с любыми типами данных. Но пока других типов нет, потому что мне они не попадались. Сделано все, что я лично использую в своей работе. Нужно отметить еще одну особенность операций rb и wb. Вообще говоря, данные надо записывать в числовые массивы i() и r(). Но указанные операции можно также использовать с массивом t(). При этом к отрицательным байтам автоматически прибавляется при чтении число 1104. Дело в том, что массив t() содержит юникоды. Первые 127 символов в обоих кодировках совпадают. А при виндовс кодировке русских букв такое прибавление числа сразу переводит их в юникоды русских букв. Исключение составляет только буква, которая произносится как ио и пишется как е с двумя точками. Я ее исключил и даже не могу ее напечатать, так как мой редактор ее не печатает. Ну а при записи из юникодов русских букв вычитается это же число. И нужно следить за тем, чтобы в тексте кроме латинских и русских букв ничего не было.
Теперь рассмотрим что делает команда #f. Вообще говоря, в эту команду можно включить сколько угодно операций, но я это делаю по мере необходимости. Нет смысла специально увеличивать размер программы и вводить операции, которые не используются. Полный список операций которые работают в версии программы на момент написания данной статьи такой: alph . cdpj . choo . copy . dele . divi . edit . edtf . fcat . find . fold . html . line . list . mb64 . modi . size . tobm . tocm . topn . tops . rep2 . repl . w2jc. Названия операций лучше всего писать полностью, так понятнее будет, и я так делаю. Я сначала перечислю что делает каждая операция, а потом просто расскажу особенности и историю некоторых из них. Точную и полную информацию можно найти в техническом описании языка. Вот ссылка .
Итак, операция fold устанавливает рабочую папку. Я уже писал об этом. Вообще говоря, первоначально я предполагал, что будут использоваться файлы только внутри папки ПИ. Поэтому рабочая папка указывает на папку внутри папки ПИ. То теперь есть исключение. Если указать имя папки null, то имеется в виду сама рабочая папка ПИ. Однако, если вторым символом в имени папки идет символ двоеточия, то используется общий адрес файла на компьютере. Указание рабочей папки -- это очень важный момент, так как полное имя файла складывается из его указанного имени, впереди которого автоматически ставится рабочая папка. Если она указана неверно, программа файл не найдет. Операция size возвращает размер файла в байтах в переменную s(1).
Операция dele уничтожает файл. Операция copy копирует несколько файлов в один файл. Операция divi выделяет из файла его часть. Название не совсем удачное. Операция fcat возвращает каталог файлов в указанной папке. Операция find ищет в файле некоторую группу байтов и возвращает результаты поиска. Операция repl тоже ищет группу байтов и просто заменяет ее на другую группу байтов в том же файле. Операция line считывает или записывает в текстовый файл одну строку текста с заданным номером.
Операция list работает с текстовым файлом и вынимает их него куски, размеченные определенным образом. Операция edit запускает встроенный редактор текстов для редактирования текстового файла. Операция html запускает встроенный браузер для показа вэб-сайтов. Браузер был написан для языка Java еще в самой первой версии. Он очень примитивный, но кое-что показывает. Одно время я его использовал, но сейчас перестал. Есть возможность использовать любой браузер. Но операция осталась и работает. Операция choo запускает специальную программу, которая позволяет пользователю выбрать любой файл с помощью менеджера файлов в файловой системе компьютера.
Про операции tobm, tocm, tops, topn я уже рассказывал в главе о картинках. Операция w2jc -- это конвертор. Я уже рассказывал про порядок байтов в разных системах. Так вот эта операция меняет порядок байтов в каждой группе из 4-х байтов. То есть если в файле записаны числа по 4 байта на каждое число, то она Виндовс порядок превратит в Java и наоборот. В 4 байта записываются целые числа и реальные формата float. Это необходимо только для передачи данных из Виндовс программ в ACL программу или наоборот. Операция alph работает с текстовым файлом. Она упорядочивает строки одного файла по алфавиту и записывает результат в другой файл. Иногда это бывает полезно, например, при составлении словарей.
Операция mb64 -- это снова кодировщик, но более специальный. В этом случае любой бинарный файл кодируется по формату mime BASE 64, который используется в почтовым машинах для передачи писем. Некоторые другие программы тоже его используют для кодирования картинок. Операция cdpj -- опять кодировщик данных из файлов, которые записывает язык Питон в системе Виндовс, в файлы, которые записывает язык Java. Он отрезает из файла первые 128 байтов и потом меняет порядок каждой группы из 8 байтов. После выполнения этой операции данные, записанные программой на языке Питон, можно прочитать в программе на языке ACL. Операция edtf запускает другой редактор для редактирования файла. Этот редактор точно эквивалентен редактору, в котором записываются программы на языке ACL в режиме разработки программ. Эта операция появилась недавно, потому что иногда это полезно.
Не все из указанных операций появились одновременно. А в будущем возможно будут и новые операции. В принципе такие операции не являются базовыми операциями языка программирования. Потому что программы для их реализации можно написать даже на языке ACL. Но они будут долго работать. Удобно иметь их уже в готовом виде, то есть написать на языке ПИ. Это в любом виде облегчает программирование. Подробности использования всех команд есть в техническом описании. Я просто отмечу для чего была сделана операция (list). Она позволяет работать со словарями. Допустим у вас в файле записаны пары (имя|содержание). А вы хотите составить оглавление имен. Вот эта операция и позволит вам быстро это сделать.
А операция (divi) рассматривает содержание файла как двумерную матрицу данных. И она вынимает из нее подматрицу. Делается это так. Пропускается некоторое число байтов n1, потом берется число байтов w, потом пропускается число байтов W и снова берется число байтов w, и так h раз. В результате из матрицы с размерами W, H вынимается матрица с размерами w, h и со сдвигом nv=int(n1/W) по вертикали и nh=n1-nv*W по горизонтали. Такую операцию запросто можно было бы запрограммировать на ACL, но просто иногда бывают очень большие файлы и не все форматы записи удобно записывать в массив r(). Эта операция была сделана в самом начале, когда возможности массива r() были ограничены.
10. АРХИВЫ ФАЙЛОВ. МНОГО В ОДНОМ И КОМПАКТНО.
Я уже писал, что файлы очень полезны для обмена информацией. Они легко копируются и передаются. Но это тогда, когда файл один. А если их много или даже очень много, то проблемы все же остаются. Естественно, что с самого начала эпохи существования файлов стали думать о том, как сделать так, чтобы их было меньше. Самый естественный путь -- это складывать много файлов в один файл, организуя в нем разметку таким образом, чтобы можно было всегда развернуть все назад. Работать с архивами программы не могут, будет очень медленно. Но для передачи файлов через электронную почту или интернет весьма полезно иметь такую возможность. Даже для целей долгого хранения файлов.
Я также уже писал, что с самого начала придумывали способы сжатия информации определенного типа, например, картинок или музыки. А особенно видео, когда файлы в оригинале имеют огромные размеры. Сжатие файлов определенного типа имеет свою специфику и существует много алгоритмов как это делать. Но и архивы тоже хотелось бы сжимать. И эти методы сжатия не должны зависеть от того, что конкретно записано в файле, потому что в архиве могут быть записаны файлы самого разного типа. Если есть проблема, то всегда найдется какое-то решение. Причем решений таких было найдено много. И сейчас их много используется.
Но в какой-то момент авторам разных проектов приходилось выбирать. И по каким-то причинам был выбран формат zip для работы с архивами. Так современные версии операционной системы Виндовс работают с zip архивами как с папками. Они их также размечают и к ним применимы все операции, которые используются с папками. Фактически тут ничего сложного нет. Современные ноутбуки уже настолько быстрые, что файлы из архива реально вынимаются во временную папку, с этой папкой можно работать. А при закрытии файла архива эта папка снова кодируется в файл архива.
Язык Java появился в 1995 году. Если честно я не знаю в какой-момент там сделали операции работы с zip архивами. Когда я начал работать на Java в 2003 году, они уже были. А язык ACL какие-то операции, которые делает Java просто по другому записывает, но делает то же самое, практически без изменений. Точнее не так. В языке Java все делается намного сложнее. Я специально следил за тем, чтобы та же самая работа записывалась не только компактно, но и проще. Ну и возможно в языке Java возможностей больше, я использовал только самые необходимые. Команда так и называется zip. Точнее можно писать одну букву #z, но я пишу полностью. У нее есть 5 операций. Рассмотрим их по очереди.
Операция #z [op=cat; file=;] позволяет получить список файлов внутри рассматриваемого zip-архива, на который указывает параметр file. Полный список файлов печатается в массив t(), с начала, которое определяется, как обычно при печати, параметром s(3). После операции параметры s(4) и s(5) показывают начало и длину произведенной записи. Имена файлов в этом списке разделяются символом вертикальной черты (СВЧ). При этом файлы внутри папок имеют сложные имена типа (folder/file), и, кроме того, есть имена типа (folder/) которые указывают на наличие самих папок. Имя файла архива нужно задавать полное относительно интерпретатора, включая расширение. Но расширение файла не обязательно должно иметь вид (zip) и может быть любым или вовсе отсутствовать. Это касается и всех других операций.
Операция #z [op=sfo; file=; n=;] FT FT . . . позволяет создать новый zip-файл, имя которого будет определяться параметром [file] и который будет содержать все файлы внутри указанных папок. Число папок указывается в параметре [n], а имена папок являются аргументами со структурой FT (форматированной строки). Все имена отсчитываются от главной папки интерпретатора, то есть рабочая папка не используется.
Операция #z [op=gfo; file=; n=; mo=;] FT FT . . . является обратной к предыдущей. Она позволяет вынуть из zip-архива все файлы из указанных папок. Структура параметров и аргументов та же, что и у предыдущей операции. Однако здесь есть дополнительный параметр [mo]. Если [mo=0;], то вынутые папки будут добавлены к существующим папкам или будут созданы новые папки, если они не существовали. Существующие файлы с теми же именами будут заменены на новые. И все новые файлы останутся на месте после окончания работы ПИ. Если [mo=1;], то вынутые файлы будут уничтожены после окончания работы интерпретатора. В этом случае вынутые файлы живут только в течение времени, когда живет сама ПИ (не путать с ACL программой).
Наконец, если [mo=2;], то вынимание файлов из архива будет происходить только в том случае, если вынимаемые папки отсутствуют на компьютере. Более точно, будут созданы только такие папки, которых не было ранее. И после работы ПИ эти папки будут существовать. Поэтому программа может вынуть такие папки только один раз. Этот режим удобен для организации дистрибутива. Важно иметь в виду следующее. Если папки вложены друг в друга, например, "one/two/...", то прежде чем вынимать внутреннюю папку, надо сначала вынуть внешнюю папку. Внутренняя папка вынимается только в том случае, если внешняя уже существует. Более конкретно, надо сначала вынуть папку "one". При этом будут вынуты все файлы из этой папки, но не внутренние папки. И затем еще одной командой нужно вынуть папку "one/two".
Операция #z [op=sfi; file=; n=;] FT FT . . . позволяет создать новый zip-файл, имя которого будет определяться параметром [file] и который будет содержать все файлы, указанные как аргументы. Если имя некоторого файла имеет структуру "folder/file", то будет создана новая папка внутри zip-архива. Эта команда является более общей по сравнению с [op=sfo;] но программисту необходимо сформировать длинный список имен, содержащих все файлы. Зато она удобна для архивирования с сжатием одного большого файла.
Операция #z [op=gfi; file=; n=; mo=;] FT FT . . . позволяет вынуть все файлы, указанные как аргументы. Файлы внутри папок должны иметь имена типа "folder/file". Параметр [mo] имеет тот же самый смысл, как и в операции [op=gfo;]. Аналогично предыдущей команде, вынимаются файлы только из последней внутренней папки (при этом она создается), а внешние папки должны существовать или быть созданы заранее.
Должен честно сказать, что я ни разу не создавал файлы архивов таким способом. Но вот вынимал файлы из архивов много раз. Более того, сама ПИ -- это файл ACLm.jar, и это zip архив. Также к ПИ можно прибавить другие zip архивы. Инргда бывает удобно файлы картинок в презентации или слайд-шоу записывать в zip архив, и ACL программа может с ним работать. Архивами zip формата являются не только Java программы, но и документы формата docx программы Майкрософт Офис. К сожалению сайты интернета не кодируются в zip-архивы, но на то видимо есть свои причины. Браузеры должны работать быстро. И также есть поисковики, которые не умеют работать с сайтами в виде zip-файлов. Но у сайтов интернета есть свой способ все записывать в один файл.
Короче, архивы -- это хорошо, особенно для передачи информации. И все еще впереди, может и я начну их шире использовать. А возможно другим людям это будет просто нужнее, чем мне. На самом деле ПИ при каждом включении смотрит внутри своего файла ACLm.jar, который является архивом, файл start.acl. Самый первый раз он вынимается и остается в папке. Но программа все равно его смотрит каждый раз при включении, потому что там есть важная информация, которая ей необходима для работы. Дело в том, что сама ПИ может работать в разных режимах и вот это как раз она и смотрит. Но об этом будет написано в другом месте, если будет.
11. РАБОТА С ТЕКСТОМ. НАДО ПОНЯТЬ ЧТО НАПИСАНО.
Первоначально текстовый массив t() играл очень ограниченную роль и приходилось обрабатывать большие тексты прямо в файлах. Это потому, что компьютеры были слабые и сильно увеличивать объем оперативной памяти, необходимый для программы, не очень хотелось, да и было просто невозможно. В современной версии я увеличил размер массива t() до двух миллионов символов, и это уже достаточно для работы с большими текстами прямо в памяти. С другой стороны, это всего лишь 4 мегабайта, совсем не так много. Работа с разбором текста, в основном, нужна для обработки информации, поступающей от пользователя программы, но могут появиться и другие применения.
Как обычно, я сделал лишь то, что лично мне понадобилось для работы. Возможности есть, но только самые необходимые. Команда, которая работает с текстовым массивом называется te, то есть начальные буквы слова text. Минимум две буквы необходимы. Она имеет 8 операций, плюс еще одна операция сделана как другая команда. Многие операции дублируют работу с файлами и их можно выполнить командой . . . . . #f [file=here;]. Первоначально все так и делалось. Но потом я решил, что это получается некрасиво и писать лишние буквы не захотелось. И вот появилась эта новая команда. Рассмотрим ее операции по порядку.
Первая операция #te [op=find; b=; le=; n=; c=;] сканирует часть массива t() начиная с индекса [b] и c длиной [le]. Она определяет все положения символа, юникод которого равен [c]. Результат в виде индексов массива t() записывается в целый массив i() начиная с первого индекса, равного значению [n]. Число повторений этого знака возвращается в параметр s(1). Как видим, все просто, но весьма важно. Чаще всего приходится искать юникоды с номерами 10 (признак конца строки) и 124 (символ вертикальной черты), так как они используются как разделители текста на блоки.
Вторая операция #te [op=repl; b=; le=; c=; mo=;] сканирует часть текстового массива начиная с индекса [b] и с длиной [le]. Она заменяет все символы с юникодом [c] на юникод [mo]. Первые 127 юникодов равны ASCII кодам первой таблицы символов. Команда #f умеет заменять в файле много символов на много символов. Но замена одного символа на другой приходится делать чаще и нужно делать быстрее. Например, часто символ 10 заменяется на 32, то есть признак конца строки на пробел. Можно его заменять и на символ вертикальной черты. И вообще эта команда как бы для символов -- разделителей полей.
3-я операция #te [op=trim; b=; le=; n=;] сканирует часть текстового массива начиная с индекса [b] и с длиной [le]. Она находит части текста, окруженные пробелами, и их координаты записывает в целый массив i(). Если таких частей несколько, то возвращаются все. Результат анализа записывается в целый массив i() начиная с первого индекса [n]. Пусть [n=k;]. Тогда i(k) будет равно первому элементу первого куска, что может быть использовано как значение параметра [b], и i(k+1) будет равно длине этого куска, что может быть использовано для задания параметра [le]. Если существует два куска, то i(k+2) будет равно началу второго куска, а i(k+3) длине второго куска. Полное число кусков показывает параметр s(1). Эта команда часто используется при обработке входных данных из текстового файла на одной строке, когда разделителем служит любой число пробелов.
4-я операция #te [op=show; b=; le=;] FT полностью аналогична команде #f [op=edit; file=here; mo=-1; c=1, ...]. Она показывает часть текстового массива, начиная с индекса [b] и с длиной [le] в редакторе текста без возможности его редактировать. Эту команду можно использовать как более простую запись команды #f. Все детали можно посмотреть в описании указанной команды. Так параметр s(1) в начале задает стартовую позицию курсора, а в конце возвращает позицию курсора перед выходом из редактора. Имя окна редактора указывает аргумент команды -- форматированный текст.
5-я операция #te [op=edit; b=; le=;] FT полностью аналогична команде #f [op=edit; file=here; mo=-2; c=1; ...]. Она показывает часть текстового массива, начиная с индекса [b] и с длиной [le] в редакторе с возможностью отредактировать текст. Эту команду можно использовать как более простую запись команды #f. Все детали можно посмотреть в описании указанной команды. Так параметр s(1) в начале задает стартовую позицию курсора, а в конце возвращает позицию курсора перед выходом из редактора. Имя окна редактора указывает аргумент команды - форматированный текст. Отредактированный текст будет снова записан в текстовый массив, начиная с индекса, указанного параметром s(3). Как обычно, после записи параметры s(4) и s(5) указывают начало и длину проведенной записи.
6-я операция #te [op=tail; b=; le=;] сканирует часть текстового массива начиная с индекса [b] и длиной [le] и изменяет значение параметра [le] таким образом, что символы пробелов на конце, а также символы '\n' или '\r' отсекаются. При этом [le] = s(10) либо остается прежним либо уменьшается. Эта операция тоже помогает обрабатывать входную информацию, которую пользователь записывает в окна ввода.
7-я операция #te [op=fitt; b=; le=; n=; c=; tw=;] сканирует часть текстового массива начиная с индекса [b] и c длиной [le]. Операция определяет все положения заданной последовательности символов, аналогично операции find, но в данном случае строка юникодов, которая ищется начинается с индекса [c] и имеет [tw] символов. Результат в виде индексов массива t() записывается в целый массив i() начиная с первого индекса, равного значению [n]. Число повторений этого знака возвращается в параметр s(1).
8-я операция #te [op=emls;] FT имеет специальное назначение. Она не работает с текстовым массивом, но использует его весьма существенно. По этой причине я отнес ее к этой команде. Она отправляет письмо по электронной почте через любые почтовые серверы интернета. Естественно, что без интернета она не работает. У нее нет параметров, но зато есть очень сложный аргумент. Этот аргумент содержит 10 полей, разделенных символом вертикальной черты. Последнее, десятое поле -- это текст письма, которое будет отправлено. А первые 9 содержат необходимую информацию для работы команды. Фактически -- это ядро почтовой машины рассылки писем по электронной почте. Пример использования команды с данной операцией находится в программе emls1.acl в папке [pro] внутри папки ПИ. Там можно посмотреть что означают первые 9 полей. Эта программа является первой, где эта команда успешно используется.
Есть еще одна команда, которая работает с текстовым массивом, а именно #read или короче #rea [fir=; n=; b=; le=;]. Эта команда в определенном смысле обратная команде #pr. Она позволяет получить числа из их текстового представления. Она работает подобно команде #io [op=rf; ], но читает текст из текстового массива t(), а не из файла. Параметр [fir] определяет, как обычно, тип и первый элемент числового массива, в который будут записаны числа, [n] задает сколько чисел должно быть прочитано, [b] определяет индекс первого элемента текстового массива t(), и [le] определяет длину части текстового массива, из которой будут прочитаны числа методом сканирования. Длина обычно известна из процедуры записи чисел. Например, команда #pr сообщает об этом через параметры s(4) и s(5).
Например, часть ACL программы #pr \G a b c;\E #read [fir=i(1); n=3; b=s(4); le=s(5);] полностью эквивалентна коду # i(1)=a; i(2)=b; i(3)=c;. Эту команду удобно использовать при обработке текстов, полученных из файлов или окон ввода. Размер реально просканированной области текстового массива t() после получения всех чисел возвращается в параметре s(1). Он может быть меньше заказанного. С другой стороны, число реально прочитанных чисел при сканировании всей заказанной области равно s(2)-1. Когда текст содержит и слова и числа можно использовать команды #te [op=trim;] и далее #read только для частей с числами. Все, что при этом необходимо знать -- это структуру записи.
12. ГРАФИКА 1. ПРОСТОЙ ВАРИАНТ.
После того момента, как у компьютера появился экран, состоящий из светящихся точек (пикселей) сразу появились программы, которые на таком экране рисуют карандашом и кисточкой. Справедливости ради надо сказать, что сначала появились экраны, которые писали только текст. Там это было невозможно. Но вот в первобытную эпоху, когда результаты получали на бумагу в виде печати символов, тоже были попытки рисовать специальной системой символов. И не только картинки, но и графики. Я сам писал программы, которые так рисовали. Однако это все давно прошло.
Исторически так получилось, что на персональных компьютерах сначала появились графические программы, которые ориентировались на точки экрана в явном виде. Они рисовали рисунки на фиксированном растре. И только потом стали писать программы в так называемом векторном виде, когда рисунки можно было масштабировать произвольным образом. В языке Java первоначально появился пакет первого типа, и он продолжает работать до сих пор. А позднее появился пакет второго типа. Дело в том, что пакет первого типа проще программируется, и бывают задачи, когда его вполне хватает. А пакет второго типа существенно сложнее, но зато его возможности больше.
Я перенес оба пакета в язык ACL в полном объеме и дополнительно добавил еще кое какие возможности от себя. Специфика графики в том, что тут практически нет циклов, а если и есть, то небольшие. И для графики интерпретируемый язык намного удобнее, чем компилируемый. Скорость выполнения вполне достаточная, зато скорость обратной связи намного выше. Легче перепробовать много вариантов и выбрать лучший. На компилируемых языках стараются делать большие программы, сильно нагруженные интерфейсом с пользователем. А на интерпретируемых языках это не обязательно. Можно писать программу постепенно, шаг за шагом. И фактически не обязательно хранить рисунок, достаточно сохранить текст программы, что намного компактнее.
В этой главе я рассмотрю первый вариант графики, который является более простым. Он выполняется командой #g. В названиях операций достаточно указывать 3 первых символа, но можно писать и целиком, так будет понятнее. Многие операции содержат координаты точек на плоскости рисунка, указывающие размеры объектов и их положение на рисунке. Я немного усложнил подход и ввел перенос и масштабирование. То есть эти координаты задаются не вполне абсолютно. Есть возможность изменить весь график, как целое, без переписывания кода программы. График может быть перемещен и изменен в размерах (масштабирован). Координаты каждого элемента перед помещением на рисунок дополнительно смещаются на вектор трансляции, который задается параметрами [trx] и [try]. То есть действительная позиция элемента определяется его координатами плюс вектор трансляции. Если этот вектор не равен нулю, то все элементы, нарисованные далее, будут перемещены. Другой параметр [sca] позволяет масштабировать размеры элементов. Этот параметр измеряется в процентах, так что [sca=100;] означает исходные размеры. Если [sca] < 100, все расстояния будут уменьшены, включая как размеры, так и позиции на рисунке (но не вектор трансляций). Если [sca] > 100, они будут увеличены.
Есть и другой режим. Если [sca] отрицательно, то для масштабирования будет использовано абсолютное значение, в то время как исходные позиции не будут меняться, только размеры. То есть в первом случае весь рисунок масштабируется как целое, а во втором -- только объекты, но не их расположение. Но есть исключения. Такие объекты как [image] (картинки) и [axes] (оси) не могут быть промасштабированы по размеру (по крайней мере на данный момент). Картинки используются как есть. Что касается размеров осей, то они могут быть изменены явным заданием параметров. Очень часто оси делаются именно на картинках, поэтому неудобно менять одно без другого. Перейдем к изучению операций.
Первая операция #g [op=open; tw=; th=; col=;] открывает новый рисунок для работы. Параметры [tw] и [th] определяют полные ширину и высоту графика в пикселах экрана. Прямоугольник графика будет заполнен цветом, номер которого в массиве цветов определяется параметром [col]. Положение всех элементов в поле графика будет отсчитываться от левого нижнего угла заданной области. Эта операция должна быть самой первой, если рисунка еще нет. Но если он уже есть, то его можно продолжить операцией #g [op=cont; n=;]. Она позволяет продолжить создание рисунка, который был предварительно сохранен в памяти компьютера в массиве картинок с номером [n].
Закрыть рисунок и спасти его позволяет такая операция #g [op=close; c=; sa=; fo=;] FT. Она сохраняет полученную картинку с номером, который определяет параметр [sa] аналогично команде #w (см. главу 4). Если [sa] > 0, то картинка спасается в памяти компьютера с номером [sa]. Номер может быть в диапазоне от 1 до 100. Если [sa=0;], то картинка будет показана на экране как кнопка в отдельном окне по центру экрана. В этом случае программа ждет, когда пользователь закроет окно. Если [sa=-1;], то картинка будет показана и одновременно будет записана в файл в текущую рабочую папку, имя файла без расширения задается параметром [fo]. Если [sa=-2;], то картинка только спасается в файл без показа на экране. Аргумент FT задает заголовок окна в том случае, когда картинка показывается на экране. В других случаях его задавать необязательно, хотя конечно ошибки не будет, если его и задать. Если картинка показана на экране, то модификатор будет возвращен в параметр s(1) как значение от 16 до 27 (см. подробности в рассказе о команде #w). Также работает параметр [em]. Если он равен 0, то выполняется старый режим и картинка размещается в центре экрана, а если 1, то дополнительно параметры [xp] и [yp] указывают координаты левого верхнего угла окна относительно левого верхнего угла экрана.
Операция #g [op=text; nx=; ny=; col=; tf=; tk=; ts=; sty=;] FT создает форматированный текст на рисунке, который задается аргументом FT. Координаты текста определяют параметры [nx] и [ny]. Дополнительное условие задается параметром [sty]. Если [sty=1;], то текст помещается левым нижним углом на координаты. Если [sty=2;] текст будет помещен центральной точкой на координаты. Наконец, если [sty=3;] текст будет помещен правым нижним углом на координаты. Цвет текста определяется параметром [col]. Фонт текста задается параметром [tf], который может меняться в интервале от 1 до 5. Это номер одного из логических фонтов. Какой реальный фонт будет поставлен ему в соответствие зависит от наличия фонтов на компьютере, поэтому просто проверьте все значения и выберите подходящий.
Параметр [tk] определяет вид фонта. Он может быть равен 0 (plain) 1 (bold) 2 (italic) 3 (bold-italic). Параметр [ts] задает размер фонта в пикселах экрана. Разумные значения 12, 14, 16. Графический текст поддерживает греческие буквы, которые могут быть заданы своими юникодами. ПИ имеет встроенную программу, которая показывает все юникоды во всех фонтах, какие есть на компьютере Такую программу можно использовать для получения информации о том какие юникоды что показывают в каждом фонте. Что касается русских букв, то если операционная система позволяет набирать русские буквы переключением клавиатуры, то это будет работать и здесь. Но в любом случае русские буквы тоже можно задать юникодами.
Операция #g [op=line; nx=; ny=; col=; n=; b=;] рисует линию как последовательность многих прямолинейных отрезков. Цвет задается параметром [col]. Координаты первой точки определяют параметры [nx] и [ny]. Параметр [n] определяет число прямолинейных отрезков Параметр [b] задает индекс первого элемента целого массива i(), который содержит длины каждого отрезка в следующем порядке: x1, y1, x2, y2, x3, y3, и так далее. Каждая пара чисел задает координаты вектора, то есть разности между концом и началом отрезка. Такой порядок позволяет легко масштабировать объекты.
Операция #g [op=area; nx=; ny=; col=; n=; b=; mo=;] рисует область. Она аналогична предыдущей операции, но в этом случае добавляется дополнительный отрезок из конца последнего отрезка в начало линии, то есть линия всегда описывает замкнутую область. Если [mo=0;], то область заполняется цветом согласно номеру [col]. Если [mo=1;], то линия представляет границу области с тем же цветом.
Операция #g [op=rect; nx=; ny=; wid=; hei=; col=; mo=;] рисует частный случай области, а именно, прямоугольник, ширина и высота которого определяются параметрами [wid] and [hei]. Центральная точка прямоугольника помещается в точку с координатами [nx] и [ny]. Если [mo=0;], то прямоугольник заполняется цветом [col]. Если [mo=1;], то рисуется только граница прямоугольника тем же цветом.
Операция #g [op=oval; nx=; ny=; wid=; hei=; col=; mo=;] операция аналогична предыдущей с тем отличием, что она рисует эллипс, вписанный в прямоугольник. Все параметры имеют то же самое значение.
Операция #g [op=arc; nx=; ny=; wid=; hei=; col=; mo=; b=; le=;] операция аналогична предыдущей, но с тем отличием, что рисуется только часть эллипса, у которого стартовый угол задается параметром [b], а угловая ширина определяется параметром [le]. Углы измеряются в градусах.
Операция #g [op=image; nx=; ny=; n=; file=;] позволяет добавить на график готовую картинку. Центральная точка картинки будет иметь координаты [nx] и [ny], отсчитываемые от левого нижнего угла графика. Если [n] > 0, то картинка будет взята из памяти компьютера с номером [n]. Если [n=0;], картинка будет взята из файла, имя которого определяется параметром [file] относительно рабочей папки.
До сих пор все было достаточно просто, и только это базово существует в Java. Правда и тут есть мой вклад. В Java не делается перенос картинки как целое и нет масштабирования. То есть параметры [trx], [try], [sca] не работают. Они есть только в ACL. Но все это можно сделать и в Java, только надо писать код. Как раз я его и написал. Но в ACL возможности данной команды были мной расширены на более сложные программы рисования. Точнее, ничего сложного нет. Просто сделаны операции автоматического рисования графиков науки. Но не целиком, а блоками из которых можно сложить график и скомбинировать его с другими элементами.
Фокус тут в том, что вообще говоря очень много рисунков можно нарисовать просто линиями. Но нужно знать координаты точек, а это чистая математика. И можно сначала число математически вычислить весь набор координат точек на рисунке, а потом использовать уже указанные выше графические примитивы. Так можно рисовать любые объекты. Этот метод по своей логике отличается от рисования карандашом на бумаге. Там рисуют сначала одну линию, потом другую и так далее. И первоначально такой же алгоритм предлагался и компьютеру. Но компьютер -- это автомат. И он может делать по другому. Сначала получить большой массив координат точек и потом все это нарисовать в цикле. Для рисования графика функции одной переменной были созданы три операции.
Первая операция #g [op=rfun; file=; mo=; le=; nx=; ny=; b=; n=;] аргументы просто прочитывает значения функций из файла, которые затем будут показаны на графике. Числа берутся из файла, имя которого задает параметр [file]. Они должны быть записаны в файл как реальные числа в компьютерном коде (длиной 4 байта) одна кривая за другой кривой. Как и в других операциях, файл может иметь заголовок. Размер заголовка определяется параметром [le]. Данные другого формата могут быть предварительно прочитаны командой #io [file=;]. Для этого предусмотрен особый случай. Если [file=here;], то числа берутся из реального массива r(), начиная с первого индекса, задаваемого параметром [b]. Значения массива r() могут быть определены предварительно разными способами.
Число точек на одну кривую задается параметром [nx] и оно может рассматриваться как размер одной колонки в обычном представлении функций матрицей чисел. Число колонок в файле определяется параметром [ny]. Однако смысл колонок может быть разным в зависимости от значения параметра [mo]. Если [mo=0;], все колонки есть функции. Аргумент для этих функций вычисляется из минимального и максимального значений Xmin и Xmax с постоянным шагом. Значения Xmin и Xmax являются аргументами команды, которые должны стоять перед любыми другими аргументами. Если [mo=1;], то первая колонка -- аргумент, а все остальные -- функции. Число функций равно [ny]-1. Если [mo=2;], то нечетные колонки есть аргументы, а четные колонки есть функции, то есть каждая функция имеет свои аргументы. Число функций равно [ny]/2.
После чтения данных минимальное и максимальное значения аргументов и функций будет возвращено программисту в элементах реального массива r() начиная с первого номера равного значению параметра [n]. Поэтому при автоматической разметке осей эту операцию надо выполнить раньше, чем рисовать оси. А при рисовании осей использовать информацию о минимальных и максимальных значениях.
Вторая операция #g [op=axes; col=; b=; wid=; hei=; xs=; ys=; bo=; to=; st=; tf=; tk=; ts=; uni=; n=;] аргументы позволяет добавить на график прямоугольник осей координат и заголовки к нему. Размеры прямоугольника осей равны [wid] и [hei]. Цвет линий и текстов задается параметром [col] как номер элемента массива цветов. Центральная точка прямоугольника осей имеет координаты [xs] и [ys]. В случае [uni=0;] разметка осей производится из минимального и максимального значений всех аргументов и всех функций. Информация о минимальном и максимальном значениях аргумента и функции xmi xma fmi fma берется из реального массива r(), в котором номер первого элемента определяется параметром [b]. Эту информацию можно получить при выполнении предыдущей операции. В противном случае она должна быть указана, см. далее. Параметры [bo] и [to] определяют длину длинных и коротких рисок. Параметры [tf], [tk], [ts] определяют номер фонта, тип и размер текстов. Параметр [st] определяет направление рисок. При 0 они внутрь, при 1 наружу.
Третья операция #g [op=dfun; col=; nx=; ny=; mo=; b=; ms=; mk=;] позволяет программисту начертить функции внутри прямоугольника осей. Значения функций должны быть предварительно прочитаны операцией [rfun]. Цвет задается параметром [col]. Параметры [nx], [ny] и [mo] имеют тот же самый смысл, что и выше. Параметр [b] определяет индекс реального массива r(), где находятся минимальные и максимальные значения аргументов и функций, используемые для рисования осей. Эти значения должны быть точно теми же самыми, как они были определены операцией [rfun]. Однако [rfun] возвращает их в индекс [n], а здесь тот же самый индекс определяется параметром [b]. К сожалению это отличие не может быть исправлено, потому что [b] используется в операции [rfun] для других целей. Будьте внимательны при задании всех параметров в явном виде.
Первая кривая рисуется цветом, задаваемым элементом массива цветов с индексом задаваемым параметром [col]. В случае нескольких кривых каждая следующая кривая рисуется цветом, задаваемым следующим элементом массива цветов. Массив цветов определяется командой #col. Тип представления кривой зависит от значения параметра [ms], который определяет размер маркера в пикселах. Если [ms=0;], все кривые рисуются линиями единичной толщины. Если [ms] > 0, то параметр [mk] определяет тип маркера для первых 5 кривых. Это есть 5-разрядное целое число, в котором каждый разряд может иметь значения от 0 до 4. Все 5 разрядов необходимо задавать, причем левый (старший) разряд относится к первой кривой, следующий слева - к второй кривой и так далее. Например, [mk=1234;] означает линию для первой кривой (левый разряд = 0), пустой прямоугольник для второй кривой, сплошной прямоугольник для третьей кривой, пустой круг для четвертой кривой, и сплошной круг для пятой кривой. Остальные кривые задаются теми же маркерами в цикле.
Указанные три операции позволяют сделать плоский график функций такого же типа, как суперкоманда ##smau, представленная в главе 6. Но здесь больше возможностей. Однако так получилось, что суперкоманды ##smau вполне хватает для работы, а представленные выше три команды я редко использую. Они были сделаны давно и их назначение перекрывается с возможностями языка постскрипт, который я использую для графиков в научных статьях. Но возможно, надо попробовать исправить эту ситуацию. Ниже представлен образец программы, в котором вычисляется функция Гаусса и затем рисуется красными маркерами. А результат выполнения этой программы показан на рисунке справа.
#d 4 A -5 0.05 0 2 1 J 101 #ma [op=vig; b=J; le=200;]
#g [op=open; tw=900; th=600; col=246;]
#g [op=rfun; file=here; mo=0; le=0; nx=200; ny=1; b=J; n=97;] -5 5 \E
#g [op=axes; col=247; b=97; wid=700; hei=500; xs=480; ys=330; bo=5; to=10; st=1; tf=1; tk=1; ts=26; uni=0; n=0;]
#g [op=dfun; col=248; nx=200; ny=1; mo=0; b=97; ms=8; mk=20000;]
#g [op=close; sa=0;] Figure\E
В команде #g реализована еще одна операция, которая рисует однозначную функцию двух переменных как аксонометрическую проекцию поверхности некоторого трехмерного объекта, описываемую однозначной функцией z(x,y) где x, y, z есть трехмерные координаты. Объект рисуется линиями через x-z и y-z сечения одновременно или раздельно. Невидимые линии не показываются. Объект помещается в координатные оси, которые показывают значения x, y и z координат. Аксонометрическая проекция строится используя точку зрения как направление между (0,0,0) точкой объекта и точкой зрения и отдельно расстояние между этими точками. Алгоритм устранения невидимых линий предполагает положительные координаты направления точки зрения около [1,1,1]. Эта операция записывается следующим образом
#g [op=axon; col=; n=; c=; b=; wid=; hei=; xs=; ys=; ts=; tf=; tk=;]
При этом цвет графика определяется параметром [col]. Полные размеры картинки задаются параметрами [wid] и [hei]. Положение левого нижнего угла имеет координаты [xsh], [ysh]. Параметры фонта для значений на осях определяются [tf], [tk], [ts] аналогично другим операциям. Функция z(x,y) задается в реальном массиве r(), начиная с первого индекса [b]. Другие реальные параметры должны быть указаны в массиве r(), стартуя с элемента с индексом [n]. Эти параметры имеют следующую структуру: xmi, xma, xfm, xdm, ymi, yma, yfm, ydm, zmi, zma, zfm, zdm, vp1, vp2, vp3, vpm, hx, hy.
Здесь [xmi] и [xma] -- это минимальные и максимальные значения на оси x; [xfm] значение для установки первой короткой риски; [xdm] значение для разности между короткими рисками. Параметры, у которых имена начинаются с y и z, означают то же самое для y и z осей. Значения [vp1], [vp2], [vp3] описывают направление точки зрения для аксонометрической проекции. Три координаты используются для удобства. Реально вектор нормируется на единицу. Расстояние до точки зрения задается отдельно значением [vpm], которое является десятичным логарифмом для избежания ввода очень больших чисел. Будьте осторожными и не вводите большие числа, так как 3 означает 1000, 5 означает 100000 и так далее. Обычно [hx]=1 и [hy]=1. Эти параметры удобны, если вместо реального трехмерного объекта желательно рисовать некую зависимость f(a,b) где [f], [a] и [b] могут иметь произвольные значения. В этом случае для получения разумной формы необходимо вводить истинные значения и затем подбирать масштабирующие коэффициенты [hx] и [hy] для x и y осей таким образом, что [da]*[hx] и [db]*[hy] имели бы значения близкие к [df] где da = [a]max - [a]min, и то же самое для [b] и [f].
Кроме того, задаются целые параметры как элементы целого массива i(), начиная с индекса [c]. Эти параметры имеют следующую структуру: nx, ny, ngv, bot, top, nxfm, nxsm, nyfm, nysm, nzfm, nzsm, nax. Здесь [nx] число точек на оси x; [ny] то же самое для оси y. Массив значений функций содержит только значения без аргументов как матрица [nx][ny]. Параметр [ngv] должен быть равен 1 (для x-z сечений) 2 (для y-z сечений) 3 (для обоих сечений одновременно). Параметры [bot] и [top] описывают длину коротких и длинных рисок в единицах, которые равны 0.001 части диагонали для x и y осей соответственно спроектированных. Может быть сделана некоторая коррекция, если [vp1] отличается от [vp2]. Параметр [nxfm] -- это номер первой короткой риски, которая преобразуется в длинную риску и получает значение. Параметр [nxsm] есть число коротких рисок между длинными рисками. Другие параметры означают то же самое для y и z осей. Последний параметр [nax] описывает появление вертикальной осей. Если [nax] = 0, левая и правая вертикальные оси появятся вместе со средней осью и горизонтальными линиями уровней. Если [nax] = 1, только правая вертикальная ось появится около оси x. Если [nax] = 2, только левая вертикальная ось появится около оси y.
Вот пример готовой программы для рисования гауссовой поверхности. В этой программе функция двух переменных предварительно вычисляется и затем рисуется операцией axon после задания всех параметров графика. Результат выполнения этой программа показан на рисунке справа от текста.
# y=-9; d=0.2; j=21; #rep 91 # x=-9; #rep 91 # r(j)=exp(-0.03*(x*x+y*y)); j=j+1; x=x+d; #end # y=y+d; #end
#p [trx=0; try=0; sca=100;] #d 6 i(1) 255 255 255 0 0 0 #col [b=1;le=2;fir=i(1);] #g [op=open; tw=800; th=600; col=1;]
#d 12 i(1) 91 91 3 7 12 2 3 2 3 1 1 0 #d 18 r(1) -0,9 0,9 -0,9 0,1 -0,9 0,9 -0,9 0,1 0 1 0 0,1 1 1 0.5 3 1 1
#p [tf=3; tk=0; ts=14; col=2;] #g [op=axon; n=1; c=1; b=21; wid=600; hei=500; xsh=100; ysh=60;]
#g [op=clos; sa=0;] Test of Graphics\E
В заключение я хочу отметить, что в главе 7 в примере программы была использована как раз такая графика. И теперь можно вернуться и посмотреть на тот пример более внимательно. Для анимации такой графики вполне хватает и она быстрее работает, чем более сложная графика следующей главы.
13. ГРАФИКА 2. СЛОЖНЫЙ ВАРИАНТ.
Пакет графики, описанный в прошлой главе развивался в то время, когда персональные компьютеры еще были весьма несовершенны. Он был ориентирован на растр, то есть на числовую матрицу с малым числом точек. В то же самое время или даже раньше развивался язык Постскрипт (Postscript), который был ориентирован на бумагу, то есть печать на бумаге и на принтеры, которые имели намного более высокое разрешение. В этом случае более предпочтительной является векторная графика, которая никак не связана с разрешением прибора, легко масштабируется и преобразуется. Основные идеи этой графики состояли в том, что надо описывать не примитивы, а более сложные объекты. И при этом не заботиться о том, как такой рисунок будет реализован.
Преимущества этой графики в том, что при увеличении числа точек растра его не надо перерисовывать. Он автоматически масштабируется на то число, какое есть. Как известно, основными элементами любой графики являются линия и область. В векторной графике линия имеет много дополнительных свойств. Она имеет толщину. При этом она имеет много способов обработки концов и углов. Она имеет структуру, в частности, может быть сложным пунктиром. Объекты описываются двумя независимыми элементами: контуром и способом закраски контура. Причем таких способов снова может быть много. Не только цвет, но и градиент цвета, а также заполнение рисунком.
Вообще говоря, с помощью пакета Графики 1 все это тоже можно сделать, но придется много и сложно программировать. А в данном пакете все это делается автоматически. Также здесь с самого начала введены преобразования. Причем не только трансляция и масштабирование. Тут есть еще и вращение и другие преобразования. А общий случай включает в себя аж 9 параметров, так называемые афинные преобразования. Понятно, что чем больше возможностей, тем сложнее ими управлять. То есть просто надо время, чтобы во всем этом разобраться. В языке Java такой вариант появился так сказать на второй стадии развития. И такую стадию одно время называли Java2. Как раз по этой аналогии я такую графику называю тоже номером 2.
Я перенес в ACL почти все, что было в Java, то есть все операции, кроме самых заумных, в которых и сам не разобрался. И часто при написании очень фасонных слайдов я эту графику использовал. Но потом я разработал более эффективную систему приготовления слайдов. Она состоит в том, что из любого документа на экране можно вырезать картинку любого размера. А потом сделать слайд как систему таких картинок. расположенных в разных местах и под разным углом. И при этом ничего не надо рисовать. Тексты можно писать в любом редакторе, хоть в Латехе, хоть в Ворде. Картинки и графики можно брать из pdf файлов или из интернета. А как преобразовывать картинки я уже написал в самом начале этой статьи.
И я почти перестал пользоваться графикой. С другой стороны, если это необходимо, то можно сделать некоторое количество суперкоманд для рисования фиксированных объектов, например, текстов на картинке, или клип, или круги и прямоугольники, а также линии. И это тоже сделано. Хотя в последней версии ПИ я резко сократил число суперкоманд, но старые можно скачать отдельно и поставить. То есть тут как бы возникает противоречие двух факторов. С одной стороны это очень интересно и тут большой прогресс для творчества. С другой стороны, все равно язык Постскрипт намного эффективнее для создания сложной графики. Более того, он ее спасает как раз в векторном виде и легко конвертируется в pdf. Там те же методы, но все вместе и проще почитать мою книгу о постскрипте и использовать его.
По этой причине я решил пока не рассказывать тут про этот пакет. Если кому интересно, попробуйте читать техническое описания языка ACL. Там этот пакет подробно описан, вот ссылка . И даже суперкоманды описаны вот тут . Но чтобы их использовать их надо сначала скачать из репозитория. Возможно в будущем я их и тут представлю, но пока нет времени.
14. РАЗНЫЕ МЕЛОЧИ, ВАЖНЫЕ В РАБОТЕ.
Для полноценной работы программы на языке ACL нужны еще кое-какие команды и операции. Это касается, в основном организации интерфейса с пользователем. Они выполняют относительно несложные операции, которые, тем не менее, часто используются. В самом начале статьи представлена команда #m (message). У этой команды есть много операций. Полезно с ними ознакомиться, так как иногда при программировании интерфейса они могут пригодиться.
Самая простая операция имеет вид #m [op=win;] FT. Она показывает текст в окне, которое ставится в центр экрана и имеет только одну кнопку [OK], клик на которой убирает ее с экрана. Сам текст является ее аргументом. Как раз мы и видели в начале статьи. Вторая операция имеет вид #m [op=yno;] FT. Она отличается от первой тем, что выставляет две кнопки с названиями [Yes] и [No]. И номер нажатой кнопки, то есть 1 или 2, возвращается в переменную &. Предполагается, что текст (аргумент) содержит вопрос, на который надо дать ответ.
Третья операция имеет вид #m [op=oce;] FT. Она отличается от первой тем, что выставляет три кнопки с названиями [OK], [Cancel] и [Edit]. И номер нажатой кнопки возвращается в переменную &. Эта форма предполагает, что пользователю сообщается какая-то информация и предлагается какое-то действие. Он может либо согласиться с действием, либо отвергнуть его, либо отредактировать само сообщение. Это может происходить при работе с какими-то информационными базами или словарями.
Эти простые операции позволяют реализовать какое-то общение. Например, вторая, то есть [op=yno;], может показывать какие-то фотографии и все время спрашивать -- продолжать или хватит. Их может быть очень много, а давать информацию о наличии разных клавиш нет возможности. Но в какой-то момент этого стало не хватать и я сделал более универсальную форму. 4-я операция #m [op=uni;] FT FT. Она имеет два аргумента. Первый, как обычно, это текст сообщения. А второй -- это несколько текстов, разделенных символом вертикальной черты. Из них первый определяет заголовок окна, а остальные -- названия клавиш, которых может быть много. Но все располагаются в один ряд. Теперь ясно, что первые три операции являются частным случаем этой. Но зато она более сложно записывается.
Через какое-то время я сделал еще более сложную команду #m [op=gen; b=; nx=; ny=; siz=; n=;] tit\E text\E butt\E. Она выставляет окно сообщения на экране вместе с произвольным числом кнопок, которые могут располагаться в несколько рядов. Аргументы команды очевидны из записи: первый задает название окна, второй - текст сообщения, третий названия кнопок. В тексте сообщения может присутствовать символ \n разделяющий строки, но строки не должны быть пустыми. Пустую строку надо задавать в виде \u32;\n. Названия кнопок разделяются символом вертикальной черты. Параметр [b] указывает индекс первого элемента целого массива i(), в котором должны быть записаны числа, регулирующие расположение элементов в окне. Число таких чисел должно быть согласовано с аргументами.
Так, если в аргументе text есть n1 строк, а параметр [n] равен n2, то чисел должно быть N=n1+2*n2. Первые n1 чисел задают размеры твердого пустого пространства, устанавливаемого после каждой строки текста сообщения. Дело в том, что строки автоматически центрируются. Если же необходимо их выравнивать по левому краю, то нужно удлинять короткие строки справа. Если же это не нужно, то можно задавать нули. Параметр [n] указывает число строк, в которые будут размещены кнопки. Поэтому следующие за n1 ровно n2 чисел, указывают сколько кнопок надо разместить в каждом ряду. Очевидно, что сумма этих чисел должна быть равна полному числу кнопок. Наконец последние n2 числа указывают размер полей справа и слева в каждом ряду кнопок. Это полезно, чтобы длина кнопок не заполняла весь ряд, что часто выглядит некрасиво.
Параметры nx, ny задают позицию верхнего левого угла окна относительно левого верхнего угла экрана. Если хотя бы один параметр отрицателен, то окно помещается в центре. Наконец параметр [siz] указывает размер полей со всех сторон окна, куда не могут попасть ни текст, ни кнопки. Как обычно, команда возвращает в [&] номер нажатой кнопки. То есть только этот вариант можно установить не в центре экрана. И именно он использован в суперкоманде с номером 33. Эта суперкоманда использовалась в процедуре scom.
В главе 3 я показывал разные формы меню, какие можно сделать на языке ACL. Но реально такие меню делает команда #ch [n=; xs=; ys=;]. Она показывает на экране картинку, заранее спасенную в шкаф (память компьютера) с номером от 1 до 100. Записать такую картинку в память позволяют команды #w , #g , #eg , которые мы уже рассмотрели. Номер картинки определяет параметр [n]. Картинка показывается как есть и без рамки. Ее положение на экране определяют параметры [xs] и [ys]. Они показывают смещение левого верхнего угла картинки от левого верхнего угла экрана в пикселах экрана. После показа картинки программа останавливается и ждет реакции пользователя. Пользователь должен кликнуть на картинке мышкой, поставив курсор мыши в нужное место, или нажать нужную клавишу на клавиатуре.
После этого картинка исчезает, а координаты курсора мыши, модификатор и код клавиши будут возвращены в программу в параметрах s(102), s(103), s(1) и s(2). Эту информацию можно использовать для последующей работы. Координаты курсора отсчитываются от левого нижнего угла картинки. Модификатором называется способ, каким был сделан клик мышкой. Можно просто кликнуть, а можно одновременно нажать какую-либо служебную клавишу. Коды клавиш и модификаторы можно узнать с помощью этой же команды, если написать простую программу на ACL.
Вообще говоря, ПИ устроена таким образом, что она может работать в трех режимах. Я описал их в самом начале. В первых двух режимах ПИ имеет собственное окно и меню. И в первый момент она может ничего не делать. Но старая версия первой программы проверяет -- есть ли в папке программы нужные рабочие папки и есть ли архив. Если чего-то нет, она вынимает папки из архива. Но уже это делает не код на Java, а ACL программа с названием start.acl. Такая программа есть во всех версиях. Причем эта программа находится внутри самой ПИ. И в первых двух версиях она при первом запуске вынимается и остается в папке ПИ. Получается два варианта этого файла. Один в архиве, другой внутри. И важны оба. Потому что первый содержит информацию, которую нельзя менять. А второй ту, которая меняется.
В информации, которую нельзя менять записано в каком виде нужно использовать программу. Если нужно использовать программу во втором или в третьем виде, то эти режимы рассчитаны на выполнение только одной ACL программы. И в этих режимах программа стандартное окно не выставляет. Во втором режиме она выставляет специальное окно, которое определяется специальным образом. А в третьем режиме она вообще никакого окна не выставляет. Точнее окно может выставить сама ACL программа -- любое какое захочет программист. В этом случае, кроме программы start.acl никакая другая программа не выполняется. И только в этом случае можно использовать команду #exit, которая закрывает ПИ.
На самом деле команду можно использовать всегда, но это приведет к закрытию ПИ. Просто это надо иметь в виду. Но бывает так, что в файле ACL программы написано очень много текста, а выполнять его не надо, но и убирать не хочется. Для таких случаев есть команда #stop. Она прекратит выполнение команд ACL в файле даже если там еще что-то написано. На самом деле можно остаток файла просто записать в процедуру и не выполнять ее. Но команда #stop еще проще. Ее можно ставить даже внутрь цикла или по условию. Она просто прекращает работу ACL программы в тот момент, когда выполняется.
В процессе работы программы бывает так, что иногда надо выставить на экран какое-то сообщение или даже много сообщений без остановки работы программы. И потом автоматически убрать его в какой-то момент. Это делают две операции команды #fr, а именно,
#fr [op=o; mo=; n=; xs=; ys=;] FT чтобы открыть окно и #fr [op=c; mo=;] FT чтобы закрыть.
Параметры xs и ys определяют позицию окна, то есть смещение из левого верхнего угла. На экране показывается картинка, заранее спасенная в шкаф (память компьютера) с номером от 1 до 100. Записать такую картинку в память позволяют команды #w , #g , #eg , которые рассмотрены ранее. Номер картинки определяет параметр [n]. Картинка показывается как есть. Если [mo] больше 0, то картинка будет показана без рамки, то есть анонимно. Она не имеет имени. Задавая разные значения параметра [mo] можно выставить разные картинки даже одну поверх другой. Это удобно в том случае, если необходима буферизация изображений для быстрой смены кадров. Всего можно выставить 10 картинок.
Основное применение этой команды состоит в показе разного рода комментариев, сопровождающих таблицу кнопок или окна ввода, устанавливаемые ACL-программой. Такие комментарии должны исчезать одновременно с окнами диалога. Другое применение -- возможность показа в автоматическом режиме серии сообщений о выполнении вычислений или другой информации, не требующей действий пользователя, в течение времени ожидания окончания вычислений. Вариант анонимной картинки можно оформить как статусную строку в нижней или верхней части экрана, которая автоматически исчезает и появляется вновь с другим содержанием. При установке таких картинок полезно знать размеры экрана дисплея. Эти размеры показывают параметры s(106) и s(107).
Если параметр [mo=0;], то картинка выставляется во внутреннем окне главного окна интерпретатора со специальным оформлением. Это внутреннее окно имеет имя и оно приклеено к окну программы. Оно исчезает и появляется вместе с ним, его нельзя свернуть или перенести за пределы окна, которому оно принадлежит, то есть окна интерпретатора. Имя определяет аргумент FT. Таких окон может быть много и они различаются по имени.
В очень большом количестве программ для пользователей можно увидеть так называемые окна ввода данных. Это такой элемент интерфейса, который использует операционная система и многие языки программирования, которые к ней привязаны, тоже используют. Язык Java не привязан к конкретной операционной системе, но в нем тоже есть такой элемент. Их неудобство для современных компьютеров состоит в том, что они не масштабируются. Как тексты с подписями, так и тексты внутри этих окон имеют фиксированный размер. Но они были сделаны давно. С тех экраны выросли в размерах, и смотреть на такие окна становится неудобно. Тем не менее в языке ACL есть команда, которая выставляет такое окно. Она записывается так
#inp [n=; le=; mo=; em=; xs=; ys=;] FT FT FT ....
И она сразу сделана таким образом, что выставляет много окон ввода. Каждое окно ввода позволяет ввести одну строку текста. Число строк определяется параметром [n]. Простейший случай [n=1;] с одним окном ввода. В этом случае панель имеет заголовок, определяемый первым аргументом FT. Комментарий к окну задается вторым аргументом FT. Наконец, третий аргумент FT содержит начальный текст, который будет введен в это окно ввода. Но если [n] > 1, то возможны две модификации задания комментариев и текстов. Если [mo] - четное число (0,2,...), то 2-й аргумент FT определяет первый комментарий, 3-й аргумент FT определяет первый текст, 4-й аргумент FT определяет второй комментарий, 5-й аргумент FT определяет второй текст и так далее. Так что в этом случае каждой аргумент FT определяет один комментарий или текст. В противоположном случае, если [mo] - нечетное число (1,3,...), то 2-й аргумент FT определяет все комментарии, отделяемые один от другого символом вертикальной черты, а 3-й аргумент FT определяет все тексты отделяемые таким же способом.
Есть также несколько модификаций размещения комментариев и окон ввода на панели. Если [mo] = 0,1, то каждый комментарий и каждое окно ввода размещаются на новой строке сверху вниз. В этом случае комментарий помещается над окном ввода. Если [mo] = 2,3,4,5, то каждая пара комментарий+текст будут помещены на одной строке, все строки образуют один столбец. Если [mo] = 6,7, то пары комментарий+текст будут помещены в два столбца. В этом случае параметр [n] должен иметь четное значение и первая половина окон ввода попадет в первый столбец, а вторая -- во второй. Если [mo] = 8,9, то пары комментарий+текст будут помещены в три столбца. В этом случае параметр [n] должен делиться на три и первая треть окон ввода попадет в первый столбец, вторая -- во второй и третья -- в третий. Если [mo] > 9, то окна ввода будут размещены по 4,5,.. в строке, но столбцы при этом не выравниваются. Последний режим я еще ни разу не использовал.
Нижняя линия панели содержит две кнопки [OK] и [Cancel]. Параметр [le] определяет длину пустого пространства с обоих сторон от этих кнопок в тех случаях, когда они размещаются в центре. Это единственный способ задать длину окон ввода, так как комментарии записываются целиком, а окна ввода не имеют размер и их длина зависит от общей ширины панели, определяемой плотной упаковкой строк с заданным размером. Такой строкой как раз и является строка с кнопками. В частности, если [mo=0;] или [mo=1;], то ширина панели зависит от максимальной длины заданных строк. С помощью параметра [le] можно сформировать любую ширину строки с кнопками. Обычно [le] = 50, но может быть больше или меньше. Значение [le] оптимизируется эмпирически. Панель в нормальных условиях помещается в центре экрана автоматически.
Содержание всех окон ввода может быть изменено пользователем. После выхода из диалога новые тексты будут помещены в текстовый массив t() аналогично команде #pr. Содержание разных окон ввода разделяется символом с кодом 10 (разделителем строк). Напомню, что индекс первого элемента для записи в массив символов t() определяется параметром s(3). После операции параметр s(4) указывает на начальный индекс первого элемента записи в t() с новым текстом (s(3) будет уже другим) и s(5) покажет длину всех записей включая и код 10 после каждой строки. Поэтому соблюдайте осторожность в работе с введенным текстом. Например, в случае [n=1;] его длина будет s(5)-1.
Если пользователь выбирает кнопку [Cancel], то текстовый массив t() не будет заполнен, а переменная [&] будет равна 2. Текстовый массив будет записан только при выборе кнопки [OK] и в этом случае [&] будет равен 1. Расположение кнопок тоже зависит от модификации. Если [mo] = 0,1 или > 5, то они расположены в центре и [le] задает пустое пространство с обоих сторон. Но если [mo] = 2,3, то они расположены в левой стороне, а все пустое пространство длиной 2*[le] справа. Если [mod] = 4,5, то они расположены в правой стороне, а все пустое пространство длиной 2*[le] слева.
Если [em=0;] то панель с окнами ввода устанавливается в середине экрана. Но если значение отлично от нуля, то положение таблицы кнопок определяется параметрами [xs] и [ys], а именно, эти параметры задают смещение верхнего левого угла панели кнопок из левого верхнего угла экрана, если [em=1;], или из левого верхнего угла главного окна программы, если [em=2;]. Последний режим удобен для приложений, запускаемых через проигрыватель и комбинируемых с внутренними окнами программы. Для проигрывателя положение и размер основного окна задается самой ACL программой. При изменении параметра [em] не забывайте обнулять его после выполнения команды.
Команда #inp позволяет также вводить пароль. Это реализуется запуском команды с [n=0;]. При этом используется только один параметр [le] для формирования длины окна и только один аргумент FT для заголовка окна. В этом случае команда выставляет одно пустое окно ввода без подписи и при вводе в него текста вместо текста показываются звездочки. Набранный текст возвращается, как обычно, в строку t() начиная с s(4) и всего [s(5)-1] символов.
Есть еще одна дополнительная возможность. Параметр [em] может быть двух-разрядным целым числом. Если старший разряд больше нуля, то есть число >= 10, то на панель выставляется дополнительная строка, имеющая четыре кнопки с именами [Help] [Notes] [Save Var] [Choose Var]. Размер этой строки достаточно большой и панель уже не может быть тоньше это размера. Но, с другой стороны, эти кнопки позволяют сразу показать пользователю возможности дополнительного сервиса. Дело в том, что для некоторых простых программ панель с окнами ввода является главной панелью программы. И хотя окна ввода подписаны, но пользователю может понадобиться дополнительная информационная помощь, которую он может сразу получить, нажимая кнопку [Help].
Далее, данные всех окон ввода представляют собой текущий вариант. Может быть много вариантов, поэтому желательно иметь способ спасти текущий вариант в базу данных или выбрать новый вариант из базы данных. Такой сервис предоставляется кнопками [Save Var] и [Choose Var]. Кнопка [Notes] позволяет вести записи комментариев по вариантам и проделанной работе. На самом деле эти кнопки просто возвращают в переменной [&] значения 3,4,5,6 и новые значения всех окон ввода. Весь описанный выше сервис программист должен обеспечить самостоятельно дополнительным кодом на ACL. Наличие кнопок только позволяет узнать о намерениях пользователя.
Честно скажу, что всеми возможностями этой команды я никогда не пользовался. А последнее время я вообще ее не использую. Я предлагаю вводить входные данные в первой строке текстового редактора, и в этом же редакторе находятся и другие варианты и подсказка как вводить входные данные. При этом не надо тыкать много кнопок и смотреть все по очереди. Как раз даже в этой команде окна ввода сгруппированы, но в старых чужих программах они распределены по всему экрану или стоят в комбинации с другими элементами. Есть программы, которые вообще имеют одно окно и в нем находится все -- и данные и результаты в разных областях. Такие программы я не люблю и это не мой стиль. Но возможность есть. Люди разные и все начинают с нуля. У каждого свой этап развития и понимания мира.
Есть еще одна важная команда, которая позволяет использовать операционную систему в работе программы. Она так и называется #sys. У нее есть всего три операции и все важны. Первая операция #sys [op=st;] запускает системные часы на компьютере (st = set time). Реально программа считывает время с компьютерных часов и запоминает. Затем можно сделать какую то работу, время выполнения которой нас интересует, и после этого операция #sys [op=gt;] считывает показания часов еще раз и разность времен между выполнением первой и второй операций записывает в переменную [$] в секундах, но точность часов миллисекунды, то есть можно смотреть число с тремя десятичными знаками (gt = get time). Все работает так, как будто вы дали отмашку бегуну и включили секундомер, а в момент финиша выключили. И смотрите время, которое секундомер показывает в переменной [$].
Третья операция более сложная. Она позволяет выполнить другую исполняемую программу прямо из ACL программы. То есть речь идет о программе, написанной на другом языке программирования, например, Java или Fortran или любом другом из сотен разных языков. Допустим у вас на компьютере есть другие программы, которые вы скачали из интернета. Вот я скачал программу TetColor.exe - это такая игра. И допустим я ее хочу запустить прямо из ACL-программы, то есть сделать на ACL менеджер файлов типа того, что есть в любой операционной системе. Операция [op=rp;] (rp == run program) как раз и запускает внешнюю программу.
Но я сделал команду с ограничением. А именно, внешняя программа запускается только в том случае, если она находится в главной папке, то есть в той же папке, что и интерпретатор. Более того, делается проверка на наличие файла, и если файла нет, то выдается ошибка. Это формально ограничивает возможности команды. Допустим, моя программа TetСolor.exe у меня установлена в отдельной папке по такому пути (D:\My Programs\Tetcolor\TetColor.exe), а интерпретатор вообще на диске C. Как быть? Решение все-таки есть. Одно из решений проблемы в ОС Windows такое. В папке ПИ записать файл с названием "runpro.bat" и с таким содержанием
D:
cd "My Programs"\Tetcolor
TetColor.exe
а в ACL программе записать такую команду #sys [op=rp; file=runpro.bat;]. Все файлы с расширением ".bat" операционная система Windows рассматривает как командные файлы, то есть исполняемые как и программы. И операция rp команды #sys их тоже выполняет команду за командой. Что касается системы UNIX, то в ней надо этому файлу присвоить атрибут исполняемого файла. Команды операционной системы необходимо выучить в другом месте. Это выходит за рамки данной статьи. Я могу порекомендовать собственную статью . В нашем bat-файле (так они называются) используется переход на диск D командой (D:), затем тривиальная команда cd (change directory) просто меняет папку на более внутреннюю по отношению к диску. Если в названии есть пробел, его надо ставить в кавычки. А название программы (exe файла) на следующей строке просто запускает файл.
Нужно помнить, что папки в Windows разделяются символом "\", а в Java - символом "/", так как язык Java был продуктом фирмы Sun Microsystems, а она делала как в UNIX. В ACL как в Java. В таком виде программа прекрасно запускается. Файл "runpro.bat" можно записать заранее (вручную). Можно даже записать много таких файлов. А можно формировать этот файл в процессе выполнения самой ACL программы перед его использованием данной командой. Это позволяет обойти указанное выше ограничение и запускать любую программу на компьютере и с аргументом. Можно делать и намного более сложные bat-файлы.
Но все так хорошо, когда после этой команды стоит, например, команда #stop. Если же команда #stop не стоит, а дальше есть еще ACL код, то ситуация сложнее. Еще сложнее если последующий ACL код нуждается в результатах расчета по внешней программе. Тогда ACL-программа должна ждать, когда закончит работу внешняя программа и только после этого продолжать работу. То есть надо как-то остановить ACL программу. Есть два способа.
Либо вызвать команду диалога, которая сама ждет реакции пользователя, типа #m [op=win;] Подождите минуту\E. Тогда ACL программа будет ждать пока вы не нажмете [OK]. Это не всегда быстро, если внешняя программа работает быстро. Либо сделать паузу на время. Можно делать много пауз, тут есть разные варианты. Паузу делает команда #rob как было показано в разделе про анимацию. Хотя на ACL можно вычислить все на свете, но есть две причины, по которым разумно сделать программу на другом языке программирования, а в ACL только использовать ее результаты. Первая причина -- у вас уже была написана программа и она хорошо работает. Зачем вам все переписывать на ACL. Вторая причина -- вам нужно очень сложный расчет сделать быстро. Тогда ACL не годится, так как он не очень быстрый, ведь команды интерпретируются. Для этой цели надо программировать на языках C, Fortran или на Java, если все аккуратно написать. Сюда же относятся программы показа кино, прослушивания музыки и так далее.
Режим работы с bat-файлом не имеет ограничений. Можно запускать программу с аргументом и даже цепочку программ одну за другой. Но записывать bat-файлы заранее не всегда интересно, а записывать динамический bat-файл -- не всегда так быстро, как хочется. В современной версии языка есть другой вариант. Если [file=arg;] то запускаемый файл записывается аргументом команды, а не через параметр [file]. При этом проверка на наличие файла не проводится, то есть реально вместо файла может быть командная строка в виде программы с аргументами, она вообще может иметь любую структуру. Такой вариант работает быстрее и устойчивее. На его основе можно написать менеджер файлов для работы со всей файловой системой компьютера. Однако сказанное выше об остановке работы ACL программы на некоторое время после этой команды остается в силе. Запуск внешней программы делается в другом потоке и чтобы он запустился надо остановить основной поток.
15. И КОЕ-ЧТО ЕЩЕ, О ЧЕМ НЕ ГОВОРЯТ.
Этот раздел заканчивает рассказ об основных возможностях языка ACL. Разумеется, что можно еще много писать о примерах кода и приемах программирования. Но тут будет именно о возможностях, которые как бы есть, но ими пользоваться не обязательно. Но раз они есть, то во всяком случае полезно о них знать. Когда я только начинал писать современную версию интерпретатора, то я был под впечатлением программы (IGOr pro). Название составлено из слов Interacted Graphically Oriented Program. И моя программа по организации весьма близка к программt IGOr pro. Там тоже программа имела окно и меню. Можно было делать рисунки, используя меню. Но был и свой язык программирования, весьма близкий к языку C. Точнее был интерпретатор этого языка.
И вот там было дополнительное окно, которое называлось терминалом, и куда программа посылала свои разные сообщения, причем они там накапливались, а не исчезали. На самом деле таких программ много. Даже в операционной системе Виндовс есть набор команд, которые вводятся через терминал. И туда же многие программы выдают сообщения. Есть терминал и в виртуальной машине Java. Точнее терминал общий, но она может в него писать. И программы на Java тоже могут туда писать. Короче, это такая стандартная штука.
И я тоже ее сделал. ПИ тоже имеет терминал. Причем в первых версиях окно терминала сразу появлялось на экране. Но потом я понял, что можно и без него, и даже лучше. И сейчас окно терминала сразу не появляется. Оно появляется по мере необходимости. Так, некоторые ошибки при выполнении программы ПИ пишет в терминал ОС. Это видно только тогда, когда сама программа запускается через терминал или через bat-файл, который его открывает. А если просто кликать ACLm.jar файл, то терминал не открывается и ошибок не видно. Некоторые такие ошибки я перенаправил на свой терминал языка ACL. И вот если такая ошибка случается, окно терминала открывается и сообщение в нем появляется.
Но ACL программы могут и сами писать в окно терминала. Для этого существует команда #m [op=txt;] FT. Самая первая такая команда открывает окно терминала и пишет в него текст, который является ее аргументом. Следующие команды просто добавляют текст к уже существующему. Но иногда бывает удобно удалить несколько символов из печати терминала. Это делает команда #m [op=rtt; n=1;] FT. Она в ранее набитом в терминале тексте удаляет столько символов, сколько указывает значение параметра [n] (в показанном варианте 1). В этом случае аргумент не используется, но он все же должен присутствовать хотя бы в пустом виде \E для соблюдения синтаксиса.
Одно из применений этой команды -- контролировать степень выполнения некоторой процедуры в цикле. Можно сначала напечатать некую строку текста, а затем по мере выполнения цикла вычеркивать символы, то есть делать обратный отсчет. Сейчас для показа степени выполнения цикла используется команда #pf , описанная в главе 7. Но она появилась не сразу. В стандартном режиме окно терминала исчезает после выполнения ACL программы. Но это не всегда бывает удобно. Бывают ситуации, когда сообщения в этом окне хочется почитать и после выполнения ACL программы. Для блокировки закрытия терминала служит команда #rob [mo=2;]. Об этой команде также говорилось в главе 7.
Есть также команда, которая широко использовалась в старых языках программирования, но потом ее объявили опасной и появилась мода обходиться без нее. Это правильно и к этому надо стремиться. Тем не менее, иногда такая команда необходима. И в языке ACL она есть. Речь идет о команде прямого перехода. В языке ACL она пишется так #go n. ПИ выполняет программу просто последовательно читая ее текст. Если встречается процедура, то положение ее текста запоминается вместе с названием, и она пропускается. При вызове процедуры текст процедуры выполняется и потом она продолжает свое путешествие с того места, на котором был сделан вызов. Данная команда перенаправляет выполнение программы в другое место, точнее на символ, номер которого указан в аргументе n.
Опасность такой команды в том, что можно легко сделать бесконечный цикл. Ее всегда надо сопровождать условием, при котором она выполняется. С другой стороны, с ее помощью можно делать собственные циклы любого фасона. Проблема также в том, что считать номера символов в тексте сложно, да и они меняются при переписывании программы. Чтобы решить эту проблему введена команда #%. Она в переменную % записывает номер второго символа в команде (тоже %) плюс 2. Потом это число можно куда то спасти и указать в команде #go n. Выглядит это так, что команда #% делает метки в тексте. А команда #go n перенаправляет выполнение программы на эти метки.
Вообще говоря, при выполнении процедур как раз и делаются такие переходы. И они точно выполняются компьютером, когда он работает по программе на своем языке. Но людям свойственно ошибаться. А часто переходы всегда надо делать с возвратом. Например, когда вы покупаете билет в другую страну, то обязательно туда и обратно сразу. Потому что вы не можете там оставаться дольше положенного срока. Так сделано в процедурах. А тут не так. Можно уехать и вернуться не туда. Или вообще не вернуться.
Есть не только специальные команды, но и специальный параметр. Он называется [err] и эквивалентен s(26). Этот параметр регулирует режим работы ПИ по обработке ошибок в коде программы. Изначально s(26)=0 и можно всегда работать не меняя его значения. В этом случае ошибки в тексте программы будут приводить к появлению сообщения об ошибке и остановке программы. Программист обязан исправить ошибку и запустить программу снова. Но так не всегда удобно. Если программой пользуется человек, не знающий языка ACL, то он не сможет исправить ошибку. Кроме того, могут быть элементарные опечатки при вводе текста в окна ввода.
То есть желательно иметь режим, в котором сама ACL программа обрабатывает возможные ошибки своего кода. Такой режим возникает, если параметр s(26) переопределен, например, s(26)=1. В этом случае при возникновении ошибки продолжение будет другим. Сообщение об ошибке не появится, переменной [&] будет присвоено значение 10101 и программа сделает безусловный переход на позицию (то есть номер символа текста программы), которая задается переменной [%]. Эта переменная может быть определена предварительно командой #% и просто математической операцией.
Это бывает особенно удобно, когда программа выполняет код в текстовом массиве по команде #e _text. Об этом более подробно будет написано в следующей главе. А также в любых более сложных формах интерактивного общения программы с пользователем. Например, в программе калькулятора пользователь вводит фактически код программы и она потом выполняется. Но пользователь может ничего не знать про язык ACL и программа не должна просить его исправить код программы. А именно это происходит в стандартном режиме. Данный механизм позволяет это исправить.
И последнее о чем еще не говорилось. Программы на языке ACL могут использовать звук. То есть они могут не только производить звук, то есть проигрывать звуковые файлы, но и записывать звук. Эти возможности, естественно тоже существуют в рамках того, что есть в языке Java. Но тут так получилось, что в Java операции работы со звуком были сделаны в самом начале. А потом эта индустрия стала бурно развиваться и разработчики языка Java опустили руки и перестали этим заниматься. То, что было сделано, работает, но это сильно отстало от современного состояния. Тем не менее, миди (midi) файлы отлично играются. Их использует команда анимации. Но есть и специальная команда #so, которая работает с звуковыми файлами. Однако я просто указал на это, а детали смотрите в техническом описании . У меня среди готовых программ есть одна, которая как раз это использует. Но вообще-то это редко кому надо.
16. О ПРОБЛЕМАХ РАСПРЕДЕЛЕНИЯ И ГЕНЕРАЦИИ КОДА ACL.
С самого начала развития программирования языки делились на компилируемые и интерпретируемые. Когда компьютеры были очень слабыми, вообще не было никаких языков высокого уровня. Все писалось прямо в коде компьютера. Но это очень неудобно и от этого быстро отказались. Тем не менее я лично застал это время. В 1970 году у нас в институте на компьютере M-220 был компилятор с языка Алгол, но он так тормозил, что проще было писать программу в коде компьютера, можно было больше сделать за то же время. В то время и даже много позже никто и не думал про интерпретируемые языки программирования. Наиболее массово это стало применяться после появления языков Постскрипт, Питон, Javascript. Язык Java тоже имеет интерпретатор, но он смешанный и компилятор у него тоже есть.
И тут важен такой момент -- есть ли в языке способ читать код из файла или нет. Например, в языке Javascript такой возможности нет. Там вэб-сайт может читать много файлов с кодом, но сам js код не может читать файлы с кодом. По крайней мере я такого не видел. Кажется такая же ситуация с языком Постскрипт. Он может читать код из файла, но два раза я ни разу не пробовал. В Питоне тоже относительно сложная структура и вообще про этот язык даже говорить не хочется, хотя его очень активно внедряют как самый простой и легкий. Это далеко не так.
А в языке ACL команда выполнения процедур #e устроена таким образом, что она кроме процедур может читать текст программы из текстового массива t(), и из файлов, причем с большим числом вложений, и даже из самого файла ПИ. Текст процедуры можно записать в файл, поставить его в специальную папку и вызывать как суперкоманду. Но текст одной суперкоманды может вызывать другую суперкоманду. Для безусловного исполнения кода программы из файла используется вариант #e [file=name;] _file, но можно исполнять и по условию. Это позволяет сделать программу, которая будет использовать весь ACL код, написанный за много лет.
Единственная проблема, которая при этом существует, состоит в том, что нужно в каждом файле явно указывать в программе ее рабочую папку, и потом возвращать ту папку, которая стояла до ее выполнения. Для работы в режиме отладки файл программы вызывается в редактор и затем из редактора выполняется. При этом рабочая папка устанавливается автоматически. Но при вызове кода из файла ничего автоматически не происходит. Наверно это можно было бы сделать, но не сделано. Польза от использования многих файлов в одном может состоять в том, что можно создать удобный навигатор по всем программам и обеспечить быстрый выход на нужную программу через несколько ступеней меню. Также удобно выделять полностью отлаженные и надежно работающие куски кода от вновь создаваемых кусков, в которых еще не все проверено и не все правильно
Разумеется, что и в такую структуру навигатора нужно включать только полностью отлаженные программы, в которой нет ни одной ошибки и блокированы все ошибки пользователя. Также ясно, что ни одна из программ не должна использовать команду #stop. Некоторые программы (почти все) пишутся так, что сначала идет серия процедур а в конце единственная команда #e _mpro !. Здесь важно ставить символ восклицательного знака в конце. Потому что он ограничивает список процедур. Если файл программы закончился и больше ничего нет, то и так сработает. А если файл запускается из другого файла, то будет ошибка.
В современной версии программы можно читать код из любого файла на компьютере, если имя файла начинается с буквы диска. Для файлов внутри папки ПИ нужно указывать полное имя относительно этой папки. Рабочая программа в этом случае не используется. Также осталось ограничение на размер имени файла не более 42 символа, а конструкция [file=arg;] не работает. То есть разумно все файлы с кодом ACL держать в какой-либо папке с коротким именем сразу на диске. Что касается интернета, то проще скачать блок файлов и поставить куда надо. Именно так устроен репозиторий на сайте ПИ.
В ACL есть также возможность исполнять код, который генерирует сама программа. Куски такого кода может вводить пользователь, затем программа добавляет свои куски и формирует код в массиве t(). Такой код исполняется командой #e [b=K; le=L;] _text безусловно, но можно и с условием. И в таком коде тоже можно использовать код из файла, никаких ограничений нет. Все эти возможности возникли как раз потому что используется единая память для всех программ и процедур. ПИ совершенно не важно где читать код, который она исполняет. Возможность читать код из массива t() позволяет шифровать код. Не секрет, что самым слабым местом интерпретируемых программ является доступность кода.
Разумеется, что сама процедура расшифровки все равно видна, но она может быть достаточно сложной и без подсказок с ней трудно будет разобраться. А все имеет свою цену. Трудную работу не все захотят выполнять. А если к этому прибавить, что команда может читать код из файла-архива ПИ, то это еще больше усложняет задачу. Конечно, за все надо платить. У ACL есть и минусы. Очень сложно распределять память так, чтобы все работало без ошибок. Но для этого можно придумать достаточно эффективные алгоритмы программирования. И включить их в систему обучения. В последующих главах, если они будут я об этом напишу. А пока все. Прогулка по возможностям закончилась.
17. НАУЧНАЯ ГРАФИКА И СУПЕРКОМАНДЫ ЕЩЕ РАЗ БОЛЕЕ ПОДРОБНО.
В 6-й главе про научную графику написано немного. На самом деле на такое программирование в моей жизни было потрачено довольно много времени. И об этом я здесь расскажу подробнее. В самом начале работы на компьютере ее просто не было. Графики все рисовали вручную по точкам на миллиметровой бумаге. Это такая бумага, на которую была нанесена сетка линий с шагом 1 мм. И было удобно ставить точки карандашом по известным координатам этой точки. Графиков было мало и их создание было отдельной сложной работой. Тогда и фотоаппараты были плохие. А еще раньше их тоже не было и люди рисовали картины. Так вот создание графиков было сродни рисованию картин.
Но уже в 70-х годах прошлого века результаты стали печатать на широкую бумагу по 120 символов на строку. И можно было строить графики прямо в печати. Ось аргумента обычно шла поперек строки, а ось функции -- вдоль строки. Бумага в то время расходовалась в огромных количествах, но зато можно было сразу видеть результат в графической форме. То есть экономить рабочее время. В то время даже картины рисовали в печати компьютеров, а также карты распределения двумерной функции, один аргумент вдоль строки, второй поперек, а разные значения функции показывали разными символами. Интернета тогда не было и каждый изобретал программы такого рисования самостоятельно. Я тоже написал много таких программ. Были у меня и программы, когда аргумент шел вдоль строки, а функция -- поперек. В этом случае число точек аргумента не превышало 100, но обычно этого хватало. А число строк я использовал таким сколько было на одном листе. Уже не помню сколько это было.
Персональный компьютер фирмы IBM с 16-битным процессором у нас появился в самом конце 80-х годов. Примерно в то же время я купил для сына домашний компьютер с 8-битным процессором и в виде клавиатуры, точнее под клавиатурой. Результаты работы он показывал на экране цветного ТВ. Это был первый в моей жизни цветной компьютер. На работе компьютер был монохромный, но он мог печатать на принтере и имел даже операционную систему ДОС. Домашний компьютер работал на языке Бейсик и был намного проще. Написать научные программы для таких компьютеров уже было не трудно. Собственно тогда все и было сделано. Уже в 1991 году я задумал создавать свой собственный язык программирования, а в 1992 году я уже вовсю на нем работал, хотя это была еще очень пробная версия.
Собственно, идея создавать свой собственный интерпретируемый язык программирования возникла как раз из необходимости программировать графику. В то время все работали на фортране и этот язык был идеальным для расчетов. С появлением персональных компьютеров в нем появилась и графика, но программировать ее было сложно. Графика быстро исполнялась, ведь в ней нет больших циклов и она не делает сложных расчетов. Но вот компиляция кода происходила медленно, компьютеры тогда были еще слабые. А сделать график сразу хорошо не получалось. Надо было смотреть на результат и исправлять неточности. И это было медленно. Это снова было похоже на рисование графиков вручную. Нужна была одна программа, которая читает текст и исполняет его. Время на интерпретацию текста было меньше, чем компиляция кода программы.
Первую программу-интерпретатор (далее ПИ) я написал на фортране. Параллельно я изучал постскрипт и написал на фортране другую программу, которая читала входные данные, организованные снова в некий примитивный язык программирования рисунков и создавала научную графику в виде текста на языке Постскрипт. То есть она просто один текст преобразовывала в другой текст. А постскрипт -- это тоже интерпретируемый язык и он исполнялся другими программами, которые массово использовались в системе Юникс, но были и в системе ДОС. Системы Виндовс тогда еще не было.
Начиная с 1995 года мне приходилось работать и в системе Юникс тоже. Это было во время командировок в город Гренобль во Франции. И там мне такая программа очень помогла. Фортран был во всех системах, в Юникс тоже. А вот на изучение графических программ в системе Юникс у меня не было времени. Там тогда, да и сейчас, все пользовались программой GnuPlot. А я на фортране автоматически создавал постскрипт код и рисовал графики, используя программы, которые его показывали. Были там и постскрипт принтеры. Одна моя программа, написанная в такой манере, до сих пор там используется. А научная статья, написанная об этом, до сих пор цитируется и по уровню цитирования среди моих статей она уже вошла в первую десятку.
Но у фортрана не только была неудобная графика. У него также были неудобные средства создания интерфейса программы с пользователем. Это было привязано к операционной системе и использовало готовые элементы этой системы. То есть программы, написанные в системе Виндовс, не работали в Юникс. И мне пришлось поменять язык программирования. В 2003 году я выбрал язык Java. И нисколько об этом не жалею. В то время его ругали за то, что он слишком медленный. Но все это прошло. Язык появился в 1995 году и поначалу реально был медленный. Но потом его интерпретатор был усовершенствован, а компьютеры стали намного быстрее. И уже даже в 2003 году все было вполне прилично. Язык Java создавал программы, которые во всех операционных системах работали одинаково и сразу. Но это все же не совсем интерпретируемый язык. Он компилируется.
Интересно, что Питон, единственный массовый интерпретируемый язык был создан примерно в то же самое время. Меня он тогда не заинтересовал, да я и немного знал о его существовании. Это сейчас его пропагандируют в каждом утюге и предлагают для изучения даже школьникам. Тогда все было не так просто. Этот язык я изучил совсем недавно, всего три года назад. И он мне не понравился. И синтаксисом, и организацией. Он слишком сложный, а часто и просто убогий. Особенно в области научной графики. Все программы были написаны давно и сильно устарели. Впрочем это был все тот же GnuPlot. Хотя на Питоне написано огромное количество программ, пользоваться ими не удобно.
Во всех интерпретируемых языках (Питон, Постскрипт, Javascript и другие) есть процедуры, как куски кода, которым присваивается имя и потом этот кусок можно использовать просто по имени. Это очень сокращает запись и позволяет легче ее читать. Разумеется есть процедуры и в моем языке ACL. Но я пошел дальше и стал записывать куски кода в файл. И такие куски я назвал суперкомандами. Они используются в коде программы как одна процедура с разными номерами. Об этом я уже писал в самом начале. Польза от суперкоманд резко возрастает, когда они написаны в универсальном виде и имеют набор входных данных.
Универсальный код с набором входных данных -- это уже полноценная программа для пользователей. Но пользователи не знают языка и им нужны окошки с подсказками, куда надо вводить числа. Это снова очень медленно и не позволяет работать автоматически. Для суперкоманд входные данные вводятся средствами языка ACL.
Описание суперкоманд я начну с самой простой, которая имеет номер 26. Она показывает на графике любую часть реального массива r(). Вот как это делается
#d 2 r(ZZ-10) J n #e [n=26;] _scom
Чтобы не портить память входные параметры удобно записывать в конец большого массива r(), где стоят элементы, которые не часто используются в программах. Но разные версии ПИ имеют разный размер этого массива. ПИ дает информацию о том, какой у него размер в параметр s(109). ПИ в самом начале определяет переменную ZZ=s(109), и в этой переменной как раз и находится размер массива. Туда пересылаются индекс первого элемента который, показывается на графике (например J) и их число (например n). После этого n чисел можно смотреть на графике. Все остальное делается автоматически. Такая процедура весьма полезна для контроля работы программы в любом месте.
Она рисует плоский график одной функции, и на нем все определено. Но разумно иметь более универсальную программу. Такая программа имеет номер 1 и она уже была раньше представлена. Прежде, чем показать ее в работе давайте определим то, что мы будем показывать. Я напишу вот такой код
# J=101; j=J; nx=91; ny=91; y=-9; d=0.2; #rep ny # x=-9; y2=y*y; #rep nx # r(j)=exp(-0.05*(x*x+y2)); j=j+1; x=x+d; #end # y=y+d; #end
Он вычисляет функцию Гаусса от двух переменных x и y в части массива r(), начиная с r(J) и nx*ny чисел. На самом деле в языке ACL функция Гаусса вычисляется операцией команды #ma намного быстрее и проще. Но я тут решил показать, как это делается на ACL. Так как точек не так много, все делается быстро. И теперь мы покажем на графике 10 кривых из этого массива на склоне, где они меняются быстрее всего. Вот как выглядит код для такой работы
# j=J+nx*31; #d 7 A j nx 10 -9 9 247 1060 #pr smau|Plain Figure\E #e [n=1;] _scom
Результат показан на картинке справа от текста. Универсальная программа записывает параметры в переменные A, B, . . ., G и в два текста. Чтобы не портить переменные они в самой программе сохраняются в конце массива r(), а потом восстанавливаются. Но они портятся при задании входных данных и это минус. Это старая система, которой я пользовался какое-то время назад. Смысл параметров такой A -- начальный индекс двумерного массива, B -- число точек аргумента, C -- число кривых, D -- начальное значение аргумента, E -- конечное значение аргумента, F -- начальный номер цвета, G -- три младшие разряда показывают масштабирование в процентах, старший разряд указывает показывать график или нет. При этом 1 показывать, 0 -- нет. Также надо напечатать два текста, разделенные символом вертикальной черты. Первый текст -- это название файла для записи графика без расширения. Расширение всегда png. Второй текст -- заголовок над графиком.
Разметка осей все еще выполняется автоматически, но значения вычисляются из начального и конечного значений аргумента, а также из значения функций. Нужно объяснить смысл параметра F. У ПИ есть массив цветов из 256 элементов. В каждом номере запасен определенный цвет. Эти цвета можно переопределять специальной командой #col. Исходно в программе заданы цвета в конце таблицы так, что 246 белый, 247 черный, 248 красный, 249, синий, 250 зеленый и так далее. Вот эти цвета и используются.
Другой способ изобразить двумерный массив целиком без искажения масштабов на осях аргументов реализует суперкоманда с номером 2. Она позволяет делать разметку осей в явном виде. Что касается оси функции, то в стандартном варианте она не используется, но если надо, то ее тоже можно использовать. Дело в том, что функции могут принимать разные значения от очень больших до очень маленьких и выписывать такие значения не удобно. Вместо этого массив нормируется на стандартный интервал (0, 1), а минимальное и максимальное значения функции показываются над графиком. Вот как выглядит код программы, которая показана на картинке справа
#d 15 r(1) -9 9 -5 5 4 -9 9 -5 5 4 0 1 0 0.2 2 #d 6 A J nx ny 1100 44 1 #p [pa=3;] #pr smmx|Map Figure\E #e [=2;] _scom
Здесь важно описать принцип разметки осей. Ось размечается с помощью пяти параметров. Это начальное и конечное значения на оси, значение первой длинной риски, шаг до следующей длинной риски и число коротких рисок между длинными. Соответственно для трех осей получаем 15 чисел. Их можно записывать куда угодно внутри массива r(). Но я обычно оставляю первые 100 значений для это цели и массивы записываю начиная от 101 элемента. Здесь эти числа записаны с самого начала. Также надо указать 6 параметров в переменных, начиная с A, указать палитру цветов в параметре [pa] и снова два текста, которые имеют тот же смысл, что и раньше. В переменных записывается начало массива, число точек по обеим осям. В переменную D надо записать то же самое, что в переменную G в предыдущей суперкоманде. В переменной E два разряда, каждый указывает число пикселей экрана на одну точку. И последняя переменная F указывает индекс массива r(), где записана разметка осей.
Но здесь есть дополнительные возможности. Переменные D и E могут быть отрицательными и знак указывает на другой режим работы. Так если D < 0, то показывается просто голая картинка без осей. Иногда это тоже необходимо. А если E < 0, то ось функций размечается без нормировки, по указанным значениям. Размеры текста во всех командах определяются автоматически по размерам картинки. Это необходимо, потому что картинки иногда бывают очень большим или очень маленькими и задавать размеры текста каждый раз не удобно. Параметр pa в настоящее время можно задавать как 0 для черно-белых карт и 3 для цветных. Есть еще значения 1 и 2, но они как бы устарели и не такие интересные как 3.
Эти две программы были представлены в в 6-й главе. На самом деле таких суперкоманд больше и они являются просто модификациями указанных с некоторыми небольшими отличиями. Но есть и принципиально другие суперкоманды. Одна из них имеет номер 3. Она больше годится в качестве наглядной презентации, но не годится для точного измерения размеров. Кроме того, она вообще не показывает часть массива. Я перестал использовать такие картинки в научных статьях. Но в презентациях это иногда может быть полезно. Для ее использования надо писать такой код
#d 15 r(1) -9 9 -8 4 3 -9 9 -8 4 3 0 1 0 0.2 0 #d 14 A J nx ny 1060 30 1 1 1 0.06 3 1 1 9 9 #pr smma|Axonometry\E #e [n=3;] _scom
О картинках такого типа я рассказывал в 12-й главе. Но там использовался другой набор входных данных. Суперкоманда исправляет этот недостаток. Здесь используется точно такая же разметка осей, причем нормировка делается другим способом, сама функция не нормируется. А переменных используется больше, всего 14. Причем первые 4 и 6й имеют точно такой же смысл, остальные отличаются. Так 5й тоже состоит из двух разрядов. Старший разряд может принимать значения: 1 для x-z сечений, 2 для y-z сечений, 3 для сечений по обоим направлениям. Младший разряд может принимать значения: 0 для рисования двух вертикальных осей, 1 для рисования только правой вертикальной оси около оси X, 2 для рисования только левой вертикальной оси около оси Y. Переменные . G,H,I . задают координаты направления точки зрения, важны только отношения; . J . задает десятичный логарифм расстояния до точки зрения, . K, L . определяют масштабные коэффициенты для аргументов на осях X и Y при рисования поверхности в том случае, когда аргументы измеряются в других единицах; . M, N . определяют координаты для установки заголовка, отсчитываются от левого верхнего угла.
В этой программе разницу в значениях функции и аргументов можно компенсировать выбором направления точки зрения. Чем ниже z координата точки зрения, тем выше будет функция. Но алгоритм устранения невидимых линий предполагает, что все три координаты положительные. Для отрицательных координат картинка может оказаться неправильной. Если надо посмотреть что сзади, то проще инвертировать сам массив. Представленными программами арсенал способов изображения двумерных зависимостей не ограничивается. Еще в самые доисторические времена, когда графики рисовались вручную, применялась техника складывания плоских рисунков для разных функций вместе, но со сдвигом по горизонтали и вертикали, а также с устранением невидимых линий. В этом случае искажения масштабов по осям не происходило, и в то же время создавался некий эффект трехмерности.
Такие графики весьма специфичны, но иногда они тоже могут оказаться полезными. Очень давно я сделал суперкоманду, которую имеет номер 4. У нее есть специфичность, которая состоит в том, что сдвиг вправо делается ровно на целое число шагов, с которым вычислены сечения. Это связано с упрощенным алгоритмом устранения невидимых линий. По этой причине хорошо выглядят только массивы, у которых число точек по оси Y вдвое меньше, чем по оси X, или еще меньше. Я покажу пример, где показаны только половина точек по оси Y. Для нашего гауссиана, который симметричен, это не такая уж большая потеря.
Кроме того, суперкоманда сразу показывает две картинки, инвертируя массив по второму аргументу. Дело в том, что одного вида спереди при таком виде рисования явно не хватает, и нужен еще вид сзади, так как невидимые линии быстро накапливаются. Ниже показан код графиков, а еще ниже результат работы этого кода.
#d 12 A J nx 46 -9 9 -9 0 20 0 20 24 0 #pr smq3d\E #e [n=4;] _scom
Эта программа заголовок не ставит, соответственно необходимо напечатать только имя файла. При этом она делает два рисунка, добавляя к указанному имени буквы a и b. И необходимо определить 12 переменных, начиная с A и кончая L. Удобство использования переменных в том, что они сразу используются в коде суперкоманды. Как и раньше, первые 3 -- это начало массива и число точек по осям X и Y. Затем два числа -- это начальное и конечное значения аргумента по оси X, следующие два -- то же самое по оси Y. Переменная H определяет дополнительный сдвиг всей картинки вправо в пикселах экрана. Это может понадобиться если числа на оси очень длинные. Переменная I обычно равно нулю. В этом случае каждая следующая кривая сдвигается на один шаг по оси X. Но если число точек по оси X очень большое и шаг очень маленький, то сдвиг необходимо увеличить. Но переменная I должна быть целым числом, сдвиг делается только на целое число шагов.
Следующее число -- это вертикальный сдвиг каждой следующей кривой в единицах 0.001 от максимального значения всего массива. Переменная K определяет размер текста в пикселах, а последнее число указывает насколько надо расширить размер графика по горизонтали, если он не влезает в стандартный размер 900 пикселей. Дело в том, что этот размер соответствует ситуации, когда число точек по вертикали в 2 раза меньше, чем по горизонтали. Но если это не так, то нужна корректировка. Как видим аргументов не так уж и много, но они весьма специфические. Разметка осей делается автоматически. Причем осей 3. Ось первого аргумента и функции нормальные, а ость второго аргумента снова квази и разметка специфическая. Вместе с тем такие графики иногда могут быть даже более предпочтительны, чем аксонометрия, потому что они ничего не искажают.
На рисунках видны особенности данного рисунка. Так как каждая следующая кривая выше предыдущей, то монотонно возрастающие кривые требуют больше места на вертикальной оси по сравнению с монотонно убывающими кривыми. Собственно такого же типа эффекты мы видим и в реальной жизни. А видимость данных графиков существенно зависит от выбора смещений каждой следующей кривой.При одной и той высоте рисунка нарастающие кривые получаются ниже, убывающие выше. Такие рисунки хорошо выглядят, когда кривых мало и они даются с крупным шагом по второму аргументу.
.